SUMMARY
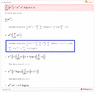
The derivative of e^(x^x) with respect to x can be computed using the chain rule and properties of logarithms. Participants in the discussion utilized WolframAlpha for initial calculations and highlighted the importance of recognizing both variables as x. The conversation also explored alternative methods, including taking the natural logarithm of both sides to simplify the differentiation process. The application of partial derivatives and the chain rule was emphasized as essential for solving this problem.
PREREQUISITES
- Understanding of chain rule in calculus
- Familiarity with partial derivatives
- Knowledge of exponential functions and logarithms
- Experience with computational tools like WolframAlpha
NEXT STEPS
- Study the application of the chain rule in multivariable calculus
- Learn about partial derivatives and their significance in calculus
- Explore the properties of logarithmic differentiation
- Practice using WolframAlpha for complex derivative calculations
USEFUL FOR
Students studying calculus, mathematicians interested in advanced differentiation techniques, and educators seeking to explain the derivative of complex functions.