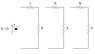
Derive a formula for equivalent resistance

Click For Summary
SUMMARY

The discussion focuses on deriving the formula for equivalent resistance in circuits with resistors arranged in series and parallel configurations. The established formulas are: for series, the equivalent resistance is calculated as Reqv = R1 + R2 + ... + Rn, and for parallel, it is Reqv = 1/{(1/R1) + (1/R2) + (1/R3) + ... + (1/Rn)}. The conversation explores the complexity of cascading multiple resistors and suggests a method for combining resistors in series and parallel to find the overall equivalent resistance. The proposed approach involves recursively applying these formulas to groups of resistors.

PREREQUISITES
  • Understanding of basic electrical concepts, specifically Ohm's Law.
  • Familiarity with series and parallel resistor configurations.
  • Knowledge of algebraic manipulation for solving equations.
  • Basic circuit analysis skills.
NEXT STEPS
  • Study the derivation of equivalent resistance in complex circuits.
  • Learn about Kirchhoff's laws for circuit analysis.
  • Explore the concept of Thevenin's and Norton's theorems.
  • Investigate practical applications of equivalent resistance in real-world circuits.
USEFUL FOR

Electrical engineering students, circuit designers, and hobbyists interested in understanding and calculating equivalent resistance in various circuit configurations.

boo_lufc
Messages
28
Reaction score
0
Is it possible to derive a formula for the equivalent resistance of n such sections in cascade?
Show your analysis.

Series: Reqv = R1 + R2 +...Rn

Parallel: Reqv = 1/{(1/R1) + (1/R2) + (1/R3) +...(1/Rn)}
 

Attachments

  • Cascade.JPG
    Cascade.JPG
    8.4 KB · Views: 570
Physics news on Phys.org
boo_lufc said:
Is it possible to derive a formula for the equivalent resistance of n such sections in cascade?
Show your analysis.

Series: Reqv = R1 + R2 +...Rn

Parallel: Reqv = 1/{(1/R1) + (1/R2) + (1/R3) +...(1/Rn)}

...and how would you go about attempting to solve this? What is the resistance of one stage? And the resistance of two stages in series? And...
 
I was thinking Rn is the last resistor so the last branch of any similar circuit would be
Rn + Rn-1 in series
Then this would be in parallel with Rn-2 + Rn-3 and so on
i.e Reqv = 1/ {(1/Rn + Rn-1) + (1/(Rn-2 + Rn-3) + (Rn-4 + Rn-5)}
Is this along the right lines at
 

Similar threads

Calculate the equivalent resistance
  • · Replies 11 ·
Replies
11
Views
2K
Total equivalent resistance of a combined circuit
  • · Replies 7 ·
Replies
7
Views
2K
Resistivity equation relating to equations for resistors
  • · Replies 23 ·
Replies
23
Views
3K
The equivalent resistance for the resistors in this circuit?
  • · Replies 5 ·
Replies
5
Views
2K
How to calculate the resistance in a combined circuit
  • · Replies 4 ·
Replies
4
Views
2K
Finding the voltage of the circuit (resistor ladder)
  • · Replies 10 ·
Replies
10
Views
2K
Determining the equivalent resistence of a circuit
  • · Replies 4 ·
Replies
4
Views
2K
Platinum resistance thermometer and Kirchoff's Laws
  • · Replies 1 ·
Replies
1
Views
3K
Modification of Wheatstone Bridge
  • · Replies 5 ·
Replies
5
Views
2K
Electrical Circuits - Parallel vs. Series
  • · Replies 14 ·
Replies
14
Views
1K