Deriving a Logarithmic Amplifier: V=ClnI

[smuscat]

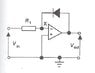
I am trying to understand the derivation of a logarithmic amplifier as shown in the figure attached.

The diode has a non linear characteristics represented by V=ClnI,where C is a constant.
Then since the current through the feed back loop is the same as the current through the input resistance and the potential difference across the diode is -Vout,we have

Vout=-Cln(Vin/R)=Kln(Vin) where R is input resistance.

What I can't understand is the step in bold,what mathematical rule is used between the two equations?

Thank you in advanced .

 

[Redbelly98]

V_out = -V_diode = _____

Can you take it from there?

EDIT:

What I can't understand is the step in bold,what mathematical rule is used between the two equations?

Just realized, there are three equations highlighted in bold. Which 2 equations do you mean?

 

[Bob S]

Write down the current across a diode as a function of the voltage (hint-it is an exponential). It turns out that an "ideal" diode is better represented by a NPN transistor, with the collector and base tied together for the anode, and the emitter for the cathode. Unfortunately, the logarithmic amplifier made from diodes has a temperature coefficient due to (kT/q) in your equation (another hint).

 

[Phrak]

Nothing adds up:

V_{out} = -C \ ln(V_{in}/R)

V_{out} = -C \ ( ln \ V_{in} - ln \ R )

V_{out} = -C \ ln \ V_{in} + C \ ln \ R \neq K\ ln \ V_{in}

In addition, why are there dimensioned units in the log argument?

You need better source material--the equation is beyond wrong.

 

[Redbelly98]

Good catch Phrak, I completely missed that

 

[smuscat]

Write down the current across a diode as a function of the voltage (hint-it is an exponential). It turns out that an "ideal" diode is better represented by a NPN transistor, with the collector and base tied together for the anode, and the emitter for the cathode. Unfortunately, the logarithmic amplifier made from diodes has a temperature coefficient due to (kT/q) in your equation (another hint).

I tried to think about it given V=clnI make I subject of the formula gives I=e^v/c but I can't go any further unfortunately.

 

[Phrak]

Good catch Phrak, I completely missed that

I seem to recall someone by the name of Redbelly guiding me out of a big whopper of a mistake not too long ago.

 

[fleem]

Vout=-Cln(Vin/R)=Kln(Vin) where R is input resistance.

What I can't understand is the step in bold,what mathematical rule is used between the two equations?

I believe the third expression has presumed R is a constant. Specifically, K is chosen for a certain R. It shouldn't be written that way (all three expression equal) because the second equals sign has that qualification (that R is a constant and its effect is included in K) but the first equals sign does not have that qualification.

In addition, why are there dimensioned units in the log argument?

Good catch. Its really a ratio with the denominator constant (at a given temperature). See http://en.wikipedia.org/wiki/Diode_modelling

 

[smuscat]

I believe the third expression has presumed R is a constant. Specifically, K is chosen for a certain R. It shouldn't be written that way (all three expression equal) because the second equals sign has that qualification (that R is a constant and its effect is included in K) but the first equals sign does not have that qualification.



Good catch. Its really a ratio with the denominator constant (at a given temperature). See http://en.wikipedia.org/wiki/Diode_modelling

First thanks for your replay

I understood your first point that R (input resistance) is included in K but I can't understand is how R is included in K.In the previous post by Phark showed that
Vout=-ClnVin+ClnR is not equal to KlnVin.Can you state the steps how you concluded that?

Sorry for my luck of understanding.
Thanks

 

[Redbelly98]

I understood your first point that R (input resistance) is included in K but I can't understand is how R is included in K.

That was what I thought at first too, but Phrak showed us that it is wrong. R could be included in an additive constant, but not in a multiplier because of the properties of logarithms.

Have you been told the diode equation, which is the basis for this discussion?

For a diode,

i = i_S (e^{V / V₀} - 1)​

where i_S and V₀ are constants for a particular diode.

But, i_S is often in the nA or pA range for many diodes, so the "-1" can be ignored when the current is much higher than that. With that approximation we have

i = i_S e^{V / V₀}​

To get the correct equation for gain in the op-amp circuit, you need to do 2 more things:

• Solve the above equation for V
• Use Ohm's law for the resisitor R to get i in terms of V_in and R

As a final step, you could also combine all the constants in the final equation into just 1 or 2 constants such as C1 and C2. Remember that R is also considered as a constant in this particular circuit.

 

[smuscat]

That was what I thought at first too, but Phrak showed us that it is wrong. R could be included in an additive constant, but not in a multiplier because of the properties of logarithms.

Have you been told the diode equation, which is the basis for this discussion?

For a diode,

i = i_S (e^{V / V₀} - 1)​

where i_S and V₀ are constants for a particular diode.

But, i_S is often in the nA or pA range for many diodes, so the "-1" can be ignored when the current is much higher than that. With that approximation we have

i = i_S e^{V / V₀}​

To get the correct equation for gain in the op-amp circuit, you need to do 2 more things:

• Solve the above equation for V
• Use Ohm's law for the resisitor R to get i in terms of V_in and R

As a final step, you could also combine all the constants in the final equation into just 1 or 2 constants such as C1 and C2. Remember that R is also considered as a constant in this particular circuit.

I tried follow the above steps by Redbelly,please tell if I did wrong or not

given I=Ise^Vout/Vo

I made Vout subject of the formula gives Vo(lnI-lnIs)=Vout

using Ohms Law did I in terms of V and R

Vo(lnVin/R-lnIs)=Vout

Vo(lnVin-lnRIs)=Vout

VolnVin-VolnRIs=V (I think that VolnRIs ~ 0 ,because Is is approx 0)

Therefore VolnVin=Vout or KlnVin=Vout

Thanks for all

 

[Redbelly98]

I tried follow the above steps by Redbelly,please tell if I did wrong or not

given I=Ise^Vout/Vo

I made Vout subject of the formula gives Vo(lnI-lnIs)=Vout

using Ohms Law did I in terms of V and R

Vo( ln(Vin/R) - ln(Is) )=Vout

Vo( ln(Vin) - ln(R Is) )=Vout

Vo lnVin - Vo ln(R Is) = V

Looks good up to here.

(I think that Vo ln(R Is) ~ 0 ,because Is is approx 0)

Not quite. If Is is "≈0", then ln(R Is) would tend to -∞, not zero.

As I see it, the ln(R Is) term should be kept, and perhaps incorporated into a single constant if you wish. This does disagree with the equation given in Post #1.

 

[smuscat]

Thank you for your replay the final answer is I think VolnVin-C=Vout

Might the equation be KlnVin=Vout or VolnVin=Vout for a particular R I think?
In other words Voln(RIs)~0

Thank you for your help!

 

[Redbelly98]

Technically yes, for a particular R in suitable units ... but this would not be a practical value for R.

We would need R Is = 1, in some system of units, for the ln to be zero. But for realistic values of Is of 10^-12 to 10^-8 Amps, R would have to be between 10⁸ to 10¹² ohms! It's simply not practical to use such large resistor values in most circuits.

So there really needs to be a constant term added (or subtracted) in the expression.

 

[smuscat]

Thanks to everybody, many thanks in particular to Redbelly98.
Gooday!