lightlightsup
- 100
- 11
- Homework Statement
- Given all the other variables in this equation, find theta.
- Relevant Equations
- Y = x(tanθ)-[(gx^2)/(2(v0cosθ)^2)]
Perhaps I should ask this question in the math section of these forums.
But, I'm stumped and I don't think this equation is solvable?
Find theta given all the other variables:
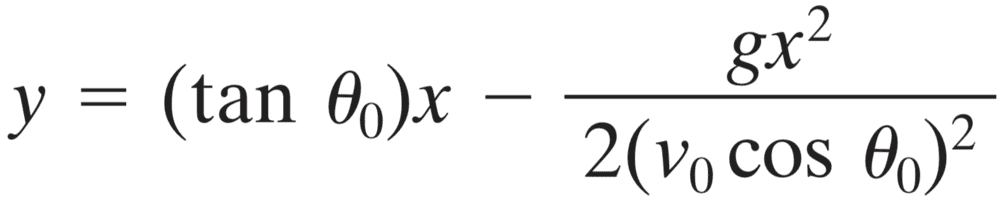
But, I'm stumped and I don't think this equation is solvable?
Find theta given all the other variables:

