Jeroen Staps
- 36
- 0
Moved from a technical forum, so homework template missing
Hi,
I am studying the behaviour of a pulley that is attached to a sling. The situation looks like this:
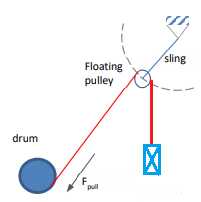
There is a drum that can give or take cable. Then there is a floating pulley with a cable through it. The pulley can move on the circle with a radius the same as the length of the sling. At the end of the cable a load is attached.
The following parameters are known:
- location of the drum
- length of the sling
- weight of the load (so you also know the gravity working on the system)
- location of the fixed point at the sling
- % friction in the pulley
The question is how the position of the floating pulley changes when a certain force is acting on the cable at the drum.
Anyone an idea on how to solve this problem?
I am studying the behaviour of a pulley that is attached to a sling. The situation looks like this:
There is a drum that can give or take cable. Then there is a floating pulley with a cable through it. The pulley can move on the circle with a radius the same as the length of the sling. At the end of the cable a load is attached.
The following parameters are known:
- location of the drum
- length of the sling
- weight of the load (so you also know the gravity working on the system)
- location of the fixed point at the sling
- % friction in the pulley
The question is how the position of the floating pulley changes when a certain force is acting on the cable at the drum.
Anyone an idea on how to solve this problem?
 ##\qquad## !
##\qquad## !