SUMMARY
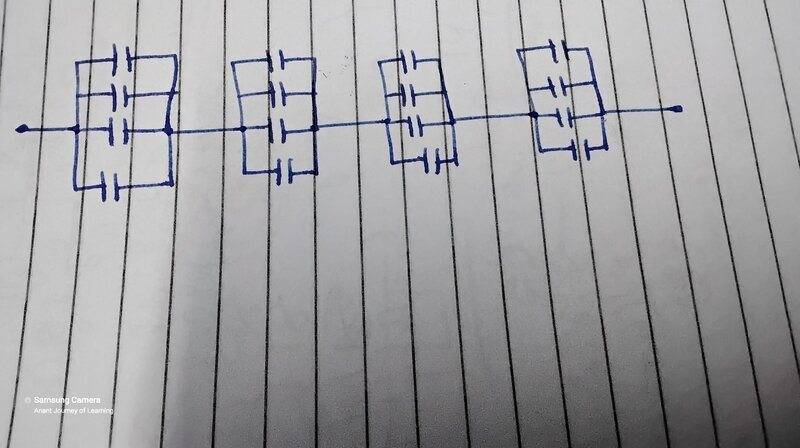
This discussion focuses on the design considerations for combining capacitors, specifically evaluating two approaches: a series array of capacitors in parallel and a parallel array of capacitors in series. Both methods are valid, but their effectiveness depends on the failure modes of the components involved. The textbook approach is preferred in scenarios where components fail open, while the parallel approach is more resilient to closed failures. Additionally, cascading failures pose a significant risk, particularly with ceramic capacitors, which are known to fail closed under overload conditions.
PREREQUISITES
- Understanding of capacitor configurations (series and parallel)
- Knowledge of failure modes in electrical components (fail open and fail closed)
- Familiarity with cascading failure concepts in circuit design
- Basic principles of capacitor behavior under overload conditions
NEXT STEPS
- Research the impact of cascading failures in electrical circuits
- Study the characteristics and failure modes of ceramic capacitors
- Explore advanced capacitor design techniques for reliability
- Learn about circuit protection strategies to mitigate failure risks
USEFUL FOR
Electrical engineers, circuit designers, and students studying capacitor applications and reliability in electronic systems.