Designing a circuit from a transfer function

Click For Summary

Discussion Overview

The discussion revolves around the challenge of designing a circuit based on a given transfer function. Participants explore various circuit topologies, component values, and the implications of their choices, focusing on operational amplifiers and their configurations. The conversation includes attempts to derive relationships between input and output voltages using superposition and circuit analysis techniques.

Discussion Character

  • Homework-related
  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • One participant expresses uncertainty about how to design a circuit from a transfer function, noting the multitude of possible solutions and seeking a systematic approach.
  • Another participant acknowledges the variety of circuit topologies and suggests that the initial structure is a good starting point, but questions the correctness of certain component values.
  • Concerns are raised about the configuration of the second op-amp and whether the expected output voltage accurately reflects the desired relationship.
  • A participant realizes that the initial circuit solution was not their own and discusses their attempts to apply superposition to analyze the circuit's behavior.
  • Discussions arise regarding the need to recalculate resistor values to achieve the correct output coefficients, particularly for the V2 input.
  • One participant proposes a new circuit design based on their understanding of the transfer function, detailing their reasoning for selecting component values.
  • Questions are raised about the necessity of certain resistors in the circuit, leading to further analysis of the V2 input configuration.
  • Participants engage in recalculating the output for V2, leading to a realization of potential errors in previous calculations.
  • Another participant presents a revised solution, incorporating feedback about resistor connections and their impact on the output voltages.
  • Disagreement arises regarding the values of resistors needed to achieve the desired output, prompting further clarification and suggestions from others.

Areas of Agreement / Disagreement

Participants generally do not reach consensus on the correct circuit design or component values. Multiple competing views and calculations are presented, with ongoing corrections and refinements to earlier claims.

Contextual Notes

Participants express uncertainty about specific resistor values and configurations, indicating that assumptions about circuit behavior may not hold under certain conditions. The discussion reflects a reliance on mathematical relationships that have not been fully resolved.

Who May Find This Useful

Students and practitioners interested in circuit design, operational amplifier configurations, and transfer function analysis may find this discussion relevant.

izelkay
Messages
115
Reaction score
3

Homework Statement


gIQbNcc.jpg


Homework Equations

The Attempt at a Solution


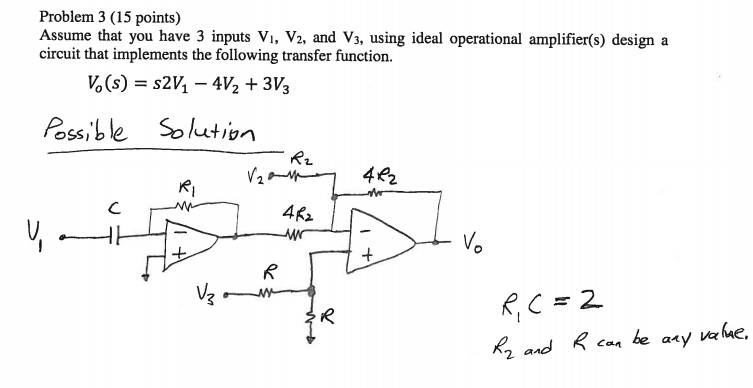
So I know how to derive a transfer function from a given circuit, but not how to design a circuit from a transfer function like the one above. It seems like there's a huge amount of possible solutions and I don't know where to begin in trying to come up with one other than guessing and checking (which would take a lot of time that I don't have on exams). Is there a systematic method or a particular approach to solve problems like this?
 
Physics news on Phys.org
Yes - you are right, there are several possible circuit topologies. And - of course - many different impedance niveaus.
But, I think, you have selected a good and simple structure, which works in priciple.
However, I am afraid some values are not quite correct.
I suppose you know about the superposition rule, which allows you to separately find the various values by setting all but one signal sources to zero?

Questions: Why 4R2 between both opamps? Recalculate this value and - as a consequence - the time constant R1*C.
 
  • Like
Likes   Reactions: izelkay
Once you remove the (+) input from ground, as you show for the second op-amp, then the (-) input is no longer a virtual earth. Have you analyzed that second op-amp arrangement to confirm the proportion of v3 in vo will be precisely what you hope it will be? :oops:
 
  • Like
Likes   Reactions: izelkay
Hey guys, thanks for your replies. I forgot to mention in my post that that solution isn't actually mine. It's my professors and I kind of just assumed it was right without checking it. It's problem 3 on this past exam:
http://www.ece.tamu.edu/~spalermo/ecen325/exam1_spring2014.pdf

If I use superposition with V1 only:

Vo = sR1CV1

V2 only:
1st op-amps output is grounded and v3 is grounded so the 2nd op amp behaves like an inverting amplifier:
Vo = -(4R2/4R2)V2
Vo = -V2

V3 only:
Vo = (1+(4R2/4R2||R2)) * V3 * (R/2R)
Vo = (1+5)V3(1/2)
Vo = 3V3So Vo = sR1CV1 - V2 + 3V3

If I did that correctly then this circuit really isn't a solution because it's missing the -4 in front of the V2 right?
 
izelkay said:
If I did that correctly then this circuit really isn't a solution because it's missing the -4 in front of the V2 right?

Yes - that`s the error. Therefore, I did recommend to recalculate this resistor between the opamps.
 
  • Like
Likes   Reactions: izelkay
LvW said:
Yes - that`s the error. Therefore, I did recommend to recalculate this resistor between the opamps.
Hm okay since I didn't come up with this particular circuit I'm going to try and start from scratch since I'm probably going to have to do this on the coming exam.

Using two op-amps as a general template:
Start with V1 on the first op-amp, and because there's an "s" there's probably a capacitor. Since it's positive and I'm using two op-amps, V1 should go into the inverting terminal of the first op amp and then into the inverting terminal of the second op amp.

With V2 and V3 on the second op-amp, since V2 has a "-4" attached to it it will go into the inverting terminal of the second op-amp while V3 will go into the non-inverting terminal.

Now it's just a matter of picking components. This is what I came up with:

QKWQTlO.png

My reasoning:
V1 only:

Vo = s(R3/R2)R1CV1

V2 only:

Vo = -(R3/R2)V2

V3 only:

Vo = [1+(R3/R2)][R4R5/(R4+R5)]V3

Looking at V2, R3 has to equal 4 R2 to get -4 in front of V2.

Looking at V1, since R3 = 4R2, R1C = 1/2 to get 2s in front of V1

Looking at V3, since R3 = 4R2, The parallel connection of R4 and R5 has to equal 3/5 to cancel out the 5 from (1+(R3/R2)) and get the 3 in front of the R3:
R4R5 = 3
R4+R5 = 5

∴ R4 = 3/R5

3/R5 + R5 = 5

R5² - 5R5 + 3 = 0

This will have two solutions, and I picked the one where R5 = 4.3, so then R4 = 0.7 (exact values included in figure).

Would this be a valid solution?
 
Is there a resistor missing for v2? As drawn the (-) input is firmly fixed at v2.
 
NascentOxygen said:
Is there a resistor missing for v2? As drawn the (-) input is firmly fixed at v2.
I made it similar to the first solution's circuit:
proxy.php?image=http%3A%2F%2Fi.imgur.com%2FgIQbNcc.jpg

where the Vo for V2 here is -(4R2/4R2) = -V2
the resistor connected to V2 didn't matter here so I thought I didn't need it in my solution.
Was that incorrect to assume?
 
Wait now that I'm looking at it again maybe I didn't calculate V2 only correctly in the original solution.

For this circuit
s%3A%2F%2Fwww.physicsforums.com%2Fproxy.php%3Fimage%3Dhttp%253A%252F%252Fi.imgur.com%252FgIQbNcc.jpg

Shouldn't V2 only be:

Vo = -[4R2 / (4R2||R2) ]*V2

= -[4R2 / 4R2R2/5R2]*V2

= -[4R2*5R2/4R2*R2]*V2

= -(20/4)V2

= -5V2

If so I'll be back later to work on my solution some more
 
  • #10
Okay here's my new solution:
EX2hoJI.png

I connected a resistor to V2

V1 only is still the same relation:

Vo = s(R3/R2)R1*C*V1

V2 only is now:

Vo = -[R3(R6+R2)/(R6R2)] * V2

V3 only is now:

(1 + [R3(R6+R2)/(R6R2)]) * [(R4R5)/(R4+R5)] * V3

If I make R3/R2 = 2, then R1*C must equal 1 to satisfy the first part.

Then, R2 = R6 = 1, and R3 = 2 to satisfy the second part

Then R4 and R5 are the same as I had them before.

Is this solution correct?
 
  • #11
Sorry - it is not. Strat with R3/R2=4
 
  • #12
Sorry - read start /instead of strat).
 
  • #13
LvW said:
Sorry - it is not. Strat with R3/R2=4
If I make R3/R2 = 4 that would cause problems for my V2 term wouldn't it?

If R3/R2 = 4:

For V2, -[R3(R6+R2)/(R6R2)] * V2 becomes

-[4(R6+R2)/R6]V2

To make this -4V2,
R6 = 1
R2 = 0
which can't be

Also sorry but could you show me what's wrong with my solution? Did I mess up on the math somewhere?
 
  • #14
For amplification of V2 you only need R3 and R6 (R2 is grounded).
 
  • Like
Likes   Reactions: izelkay
  • #15
LvW said:
For amplification of V2 you only need R3 and R6 (R2 is grounded).
Ahh okay, thanks. I think I get the general gist of it now, I just need to be careful with the connections.
 

Similar threads

Engineering Is it possible for a low pass filter to have such a transfer function?
  • · Replies 16 ·
Replies
16
Views
2K
Engineering How do I draw the Bode diagram of this transfer function?
  • · Replies 3 ·
Replies
3
Views
3K
From differential equations to transfer functions
  • · Replies 5 ·
Replies
5
Views
3K
Finding the transfer function for a difference amplifier
  • · Replies 8 ·
Replies
8
Views
2K
Circuit Requirements Questions (Design of a stadium lighting system)
  • · Replies 5 ·
Replies
5
Views
2K
Engineering How do radial tooth clutches function?
  • · Replies 6 ·
Replies
6
Views
2K
Engineering Step response and realiziability of a G(q) transfer function
  • · Replies 1 ·
Replies
1
Views
3K
How to Calculate the Complex Op Amp in Circuit Diagram
  • · Replies 8 ·
Replies
8
Views
3K
Engineering Average heat transfer coefficient (forced convection)
  • · Replies 6 ·
Replies
6
Views
3K
Engineering How to Design a Circuit from a Given Transfer Function?
  • · Replies 5 ·
Replies
5
Views
3K