Designing Inductor, need you worry about saturation?

[tim9000]

Hi,
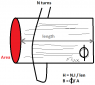
I'm just wondering (theoretically), about calculating magnetic opperating point for an inductor. Say permetivitty mu is 'u', N turns, A area, l is length:
Inductance L = u.N².A / l

Then do you need to worry about saturation? Or can you just wrap as many turns around it as you want for a massive inductance? As per that formula.
Is an inductor different to a transformer in that you don't need to worry about a magnetising curve for a type of steel?

 

[zoki85]

Then do you need to worry about saturation? Or can you just wrap as many turns around it as you want for a massive inductance? As per that formula.
Is an inductor different to a transformer in that you don't need to worry about a magnetising curve for a type of steel?

You can wrap as many turns as you want for a massive inductance, but if you don't decrease operating current magnitude accordingly, you'll saturate the core.

 

[jim hardy]

Arithmetic behind Zoki's statement:

Your formula for inductance derives from the one for flux

Φ = μNiA/l

since inductance is flux linkages per ampere, NΦ/i,

multiply both sides of flux formula by N/i and you get NΦ/i = N/i * μNiA/l = μN²A/l = L

So as you increase the turns you decrease the amps it takes to saturate the core.
Decent iron will take about a Tesla to a Tesla and a half.

 

[tim9000]

Hi,
It is this property of ferro saturation that I'm concerned with. After concidering your responses, I found a formula for max B = max Voltage/ (A.N.w)
derived from Faraday's. So in my mind I'm concidering having heaps of turn around the inductor, not decreasing the current and saturating the core. Then I think, we'll I'll increase area (A) to lower max B, but I think about the magnetisation curve where I want to push the operating point back down to the knee of the curve, from saturating. But when I think about H = N.I / length
Isn't field intensity (H) staying the same? As B comes down, so: u (mu) = B/H, thus mu is lowering with B decreasing (because flux = B.A).
It is visualising what is happening to the magnetising curve as I incrase 'A' that I can't understand, to have a fixed 'H' and a lower 'B' wouldn't the curve itself have to grow??

Thanks!

 

[jim hardy]

You're getting good at this magnetics.
It's real confusing i think because it's a field and we are accustomed to thinking of electric circuits not fields, so we are unaccustomed to including the physical dimensions.
It's worse for me because i learned it in Gilberts, Oersteds, Maxwells and Gausses. What's in a name, huh ?I assume we're talking AC here...
At some ampturns/inch you'll saturate the core regardless its area. So B doesn't come down with area it stays constant.
But the bigger the core the more the total flux so the higher the AC voltage required to push those AC amps through the turns.

That's shown by rearranging your new formula: maxVoltage = B * (A.N.w)

Volts per turn at any given frequency is proportional to total flux, B X A ., not just flux density B.
so when you locked amps you locked flux density B. When you doubled the area you doubled both total flux and volts.For DC same applies - at some amp turns per inch you'll get B webers per square meter of core, and total flux B X A webers. maybe that's best way to think of it, as DC.
After all - at any instant in time AC is unidirectional. Handy thought tool, that one.

And a handy table to copy and print - lots of magnetic sites still use the old cgs units.
http://www.magnetic-shield.com/pdf/how_do_you_measure_magnetic_fields_in_gauss.pdf

 

[tim9000]

Oh dear I am confused now. I thought I'd better do a picture just so there can be no 'crossed wires' :P
I'd never even heard of some of those cgs units. Thanks. Yep, I was talking AC.
You've pointed out that when I "locked amps I locked flux density B" which I didn't realize, so how can you move back down the curve to move the operating point to the knee from saturation by adding more steel? Surely I don't need to lower the current...I'm just thinking about huge transformers etc.

My second question is, is it ok to think of H as externally applied, fixed length, fixed turns number, fixed 'H'?

Thanks

 

[jim hardy]

so how can you move back down the curve to move the operating point to the knee from saturation by adding more steel?

well, you could add length to your iron path instead of cross sectional area. Or you can add a small air gap.

BUT - i notice your sketch shows a bar not a closed loop core. If your core is just a rod not a toroid or something, then your magnetic path is half air. Inside the coil flux travels in iron where u is hundred if not thousands, but outside your coil it's traveling in air where u is just 1.. So nearly all your MMF is expended in the air. Flux in a long solenoid will only about double when you insert the core. So, if your sketch represents your apparatus, saturation won't be a problem.

Calculate how many amp turns it takes to push 1.5 Tesla through similar lengths of air and iron.

Radio Shack sells a cheap power transformer that has a D shaped core from which you can remove an end of the D. Just pry the stamped retaining frame apart and the end piece falls out. Try an inductance measurement both with and without a sheet of heavy paper under the end piece.

Here's a paper on magnetic calculations:
http://www.ece.msstate.edu/~donohoe/ece3183magnetic_circuits_and_transformers.pdf

 

[tim9000]

I'm not physically building anying just yet, though good point about concidering a closed and nonclosed path. I am going to be doing some work on toroids though but good to know the sketch would be half air core (retun path).

Ok, so you're saying length is the only parameter I have to work with (physically changing a design), if there is no air-gap?
Otherwise I need to lower the current (or voltage), as B is foremost depenant on current, rather than area. (Ie. B = u.N.I/l locks 'B' so B_max = V/N.A.w can't lower 'B' as the 'A' is increased)

If one wished to have a large inductance, wouldn't having an air-gap be detramental (forget about linearising the curve for a moment) because it would increase the reluctance path?

Cheers!

 

[jim hardy]

You're getting there ! This is a magnetic circuits problem !

B is flux per unit area
just as J is amps per unit area, and in circuits we hardly ever use J so our thinking does not get accustomed to thinking in terms of a field..

MMF pushes flux just as an Efield pushes on charge, and MMF is proportion to amp-turns.
MMF pushes across whatever area is available, one direction inside the coil and the other way outside the coil.
That's why A is in the reluctance equation and the flux equation and the volts equation,,, more area conducts more flux.

If one wished to have a large inductance, wouldn't having an air-gap be detramental (forget about linearising the curve for a moment) because it would increase the reluctance path?

Indeed. That's why i so dislike that little Radio Shack transformer, the core is not held tightly together.

When you want a precise and predictable inductance in a closed core you include an air gap. Some adjustable inductors use a mechanically adjustable air gap.

Are you making a power transformer where you want low exciting current, or an inductor where you want constant reluctance? As you are experiencing, iron is nonlinear and a bit of air in the path will help straighten out the curve over some operating range..

 

[tim9000]

Thanks for your attention Jim. Since you didn't pull me up on that middle paragraph I'll assume that in adding steel, it only matters if it adds to the magnetic path length. But I'm still grappling with how is Area important then?

I'm actually concidering learning some finite element analysis simulation (just on my own) for some magnetics research for my 4th yr uni project next year. But magnetics is so briefly touched on, so long ago that I feel I'm practically just starting.

Are you making a power transformer where you want low exciting current, or an inductor where you want constant reluctance?

I'm a bit confused because I infer from your statement that they're kind of mutually exclusive or there is some distinction (?) I'll be concidering both, but wouldn't a transformer have a constant reluctance too? And an inductor would have a exciting (magnetising) current (ideally zero) like a transformer too wouldn't it? (just no secondary)

One issue I'm having is that I can see all the equations, but I can't get a feel for what's happening. For instance I consider increasing the area so flux = MMF / Reluctance, and since the area goes up the reluctance goes down and thus the flux goes up. And I consider B = Flux / Area, so I know both Flux and Area have gone up, but I'm wondering have they both gone up (moved) in proportion? Is that ratio stayed exactly the same? Or could it be still changing?

That statement you said about the flux traveling one way inside the material and the other outside reminded me of another question. Do you know anything about total internal confinement of the flux in a toroid? Because I didn't really feel like the Wiki article explained it (the symmetry etc.) and it sounds interesting.

Thanks heaps, appreciate your help.

 

[jim hardy]

One issue I'm having is that I can see all the equations, but I can't get a feel for what's happening.

There's the rub, eh ?
I have that trouble too. As i said in another post, the mind can believe anything so i have to constantly cross check my "feel" against the math, tuning my "feel" as i go so it leads me to the same formulas as the giants on whose shoulders we stand. My memory is awful so i have to figure out equations because i just can't remember them. But i think I'm getting along okay for the plodder i am.

My trouble came from trying to treat magnetic field the same way as circuits. In circuits we use simple Volts for E and Ohms for R and Amps I for current.
But genuine physicists seem to prefer working in E as volts per unit length and resistivity σ ohms X area per unit length (Ω x meter) and Amps per unit area, J. They have an advantage over us circuit guys in that they've already gone through the mental discipline to keep things straight, and I STILL struggle to do that.

So is MMF just a force like Voltage or a field like Volts per meter ?
Going back to that table at http://www.magnetic-shield.com/pdf/how_do_you_measure_magnetic_fields_in_gauss.pdf

MMF is AMP TURNS, analogous to Volts in circuits. I guess MMF is NI, Number of turn X Iamps.
MMF per meter is of course the magnetizing force field and that's H, NI/length.
Flux is Webers Φ and flux per meter^2 is flux density B, Teslas .
Magnetization curves are B versus H because they describe the iron not the magnetic circuit.
Permeability μ is analogous to resistivity, what flows(flux) per unit area divided by what's pushing it, MMF. (Webers/area) /(amp-turn/length ) which reduces to webers / (amp-turn x length) . It's a property of the material .

We circuit guys are accustomed to Ohm's law which uses Resistance not Resistivity.
We'd prefer to work with Reluctance and MMF but to get to reluctance we have to know the geometry of a circuit includeing its dimensions .
Let's just use ℝ for reluctance.
ℝ of a magnetic circuit is the sum of the ℝ's of its individual pieces.
Flux = MMF / Reluctance and that's ohm's law for a magnetic circuit.

But reluctance is not straightforward to calculate
and we're taught instead that B = μH which is always so.
We have to go through the exercise of calculating some reluctances for the difference to sink in.
I never had to do that until i hit a motors course.

To get to flux we have to calculate reluctance and total amp-turns and i think that's the source of your frustration. At least it was mine (circa 1966, revisited in 1980's).

I'll assume that in adding steel, it only matters if it adds to the magnetic path length. But I'm still grappling with how is Area important then?

You are making an inductor. Inductance is FLUX X TURNS/AMPERES. You've locked turns and amperes, so what is left to determine flux?
Well, Flux is MMF/ℝ . By locking amps and turns you have only ℝ left to adjust. So you can adjust ℝ by area or length of magnetic path.
More area = less reluctance, more length = more inductance.

I'm a bit confused because I infer from your statement that they're kind of mutually exclusive or there is some distinction (?)

No, just practical matter of assembly. Usually you want max inductance in a transformer so magnetizing current will be low. In an inductor you're more interested in avoiding saturation, though there are exception(saturable reactors are used in controls).

I'll be concidering both, but wouldn't a transformer have a constant reluctance too?

In transformers we usually consider them ideal for circuit analysis. But to be rigorous, the transformer core is nonlinear(B-H curve) so as it approaches saturation its magnetizing current increases and sprouts harmonics as it deviates from a sine wave. Inductor suffers from the same effect so one designs for the condition it'll see in service.

And an inductor would have a exciting (magnetising) current (ideally zero) like a transformer too wouldn't it? (just no secondary)

Yes, exactly. A transformer can be used for an inductor. But if you're using it for DC beware - it's designed for minimum reluctance so is easy to saturate. Review my example of the cheap Radio Shack transformer..

And I consider B = Flux / Area, so I know both Flux and Area have gone up, but I'm wondering have they both gone up (moved) in proportion? Is that ratio stayed exactly the same? Or could it be still changing?

It ought to be exactly the same. When you go to definition of permeability they have a caveat that flux density is uniform across the area. Remember in math everything is perfect, we are trying to align our "feel" so that it appreciates the differences between ideal and real worlds yet leads us intuitively to the equations.
So my answer is : For all practical purposes, yes it's the same.

Do you know anything about total internal confinement of the flux in a toroid? Because I didn't really feel like the Wiki article explained it (the symmetry etc.) and it sounds interesting.

Now there's a good one ! I guess you mean this article?
http://en.wikipedia.org/wiki/Toroidal_inductors_and_transformers

If i learn something every day i might know something some day !
I never before thought about that circumferential current making a single turn around the core. But of course, the wire follows the core in a curlyque so its current traverses the circle and right hand rule applies and there'll be a small MMF perpendicular to plane of toroid. But that return winding cancels it..
This is my first venture into the subject so no, I'm not familiar enough to say anything with confidence. They use vector calculus which i barely passed.
I'd always assumed toroids were so good because they can be made from a tape would core which has no gaps at all, whereas an ordinary core has to be assembled from pieces.

Whew ! Sorry to be so long winded. My motor design course is what gave me my basic magnetics - is there such a course in your curriculum ?

If you can find a paperback book by Jack M Janicke called "Magnetic Measurements" by all means buy it. Mr Janicke was a magnetics engineer(now deceased) and hobbyist who ran a small garage business in New Jersey. I built one of his differential magnetometers - what a learning experience! And fun ! His book is EXCELLENT.

old jim

 

[tim9000]

Hi Jim, I always appreciate a thurough reply, thanks.
I've thought about what you said and I think I know what you mean. I need to try and think back to when I did Electromagnetics, rederiving Maxwell's equations is a spiritual experience :p
To answer your question, I suppose it is not a force like we fall into the trap of thinking and should remember (A/m) and that MMF per meter is like a force. Good point you made some other good points that I won't revisit atm.

I see what you're saying about the Area, however I still don't jel with Faraday's: B = V / N.A.w
B is being determined by B = uNI/l
yet the Right hand side of that Faraday derivation also seems like it consists of variables you can directly infulence, as with the second equation. So what resolves the possible conflict?

Also, if you had a bar inductor, and you wanted to think of a magnetic circuit, would you just take the total path as being length of iron reluctance + length of iron (but for the reluctance of air) i.e the air path is the same length as the iron?

Yes there is an equivilant motor course for me, however it is extremely difficult to pass, the lecturer teaching it maintains that it's all simple and doesn't understand why people find it difficult, yet if you make the most minor mistake you'll get marked down horrendously.
I'll look for an Ebook of it.

Cheers Jim.

 

[jim hardy]

Well clearly I'm struggling with it still after all these years. I'm just plain awkward at math so have to keep my "feel" on course. This does me good, reviewing the units and clarifying the mental pictures. If i had it mastered i should be able to explain it all in twenty five words or less.

I still don't jel with Faraday's: B = V / N.A.w

Hmmm we probably need to talk some more on that.
In my alleged brain, i take that formula and re-arrange it as follows and my conflicts disappear:

1. Multiply both sides by A
B*A = V / N*w ( is w omega, radians.sec? if not then I'm thinking wrongly here so please apply rudder)
or Φ = V/N*w which says flux is (volts per turn) per hertz which we know to be so, it's the basis of volts/hz overflux protection schemes in machinery, no conflict yet...

2. Multiply both sides by w,
w*Φ = V/N which says rate of change of flux is volts per turn, which is at first a useless piece of trivia.
...It got driven home for me ca 1974 when i had an old three phase core at home to play with.
I was experimenting by exciting the center leg to known voltage with my variac and observing how flux divided between the other two legs. If i put a shorted turn around one of the outside legs the flux shifted over to the other outside leg to complete its loop. My plan was to saw an air gap in one leg and make a welder...
I ran a magnetization curve on it and observed saturation with my AC ammeter in exciting coil, current rises sharply of course...
That was a big core good for about two volts per turn at 60hz.
I realized quickly that volts per turn (at operating frequency) is a really handy number to know for a core. It tells you how much flux the core can handle so you know immediately how many turns you need.
That's why you'll see that funny looking term V/N*frequency in transformer core datasheets at places like Magnetics Inc. Incidentally they have a good technical library on line.

3. Multiply both sides by w,
N*w*Φ = V, the ever familiar volts equals ndΦ/dt , so there's no conflict for me.

Likely I've missed something here. I was never up to deriving Maxwell, but did sit through it in modern Physics class.

yet the Right hand side of that Faraday derivation also seems like it consists of variables you can directly infulence, as with the second equation. So what resolves the possible conflict?

Above did it for me but i may be on a different tack than you... can you expand on 'conflict' ?

if you had a bar inductor, and you wanted to think of a magnetic circuit, would you just take the total path as being length of iron reluctance + length of iron (but for the reluctance of air) i.e the air path is the same length as the iron?

That's what i do for an approximation and it works fairy well. It works really well for explaining why flux only doubles when you insert a core into a straight solenoid.
In reality some flux takes a shortcut and just surrounds part of the coil instead of traversing its whole length , but even that flux sees a part air- part iron path.Boring Anecdote time: (old guys do this)
The position of control rods in our reactor is measured by a solenoid twelve feet tall. It sits above the rods.
Rods are lifted by a steel shaft that moves up through the center of the solenoid.
The solenoid has two windings, one excited with fairly constant current and the other connected to a voltmeter.
As the reluctance of the whole twenty four foot path (12 up thru center, 12 down outside) decreases due to replacing inner 12 feet with steel, the flux goes up and the induced voltage follows suit.
Those coils were affected by nearby structural steel, and when experimenting with them in the warehouse we found they'll see rebar in the concrete floor.
Not surprisingly the system was somewhat nonlinear so the supplier made turns per foot a little more dense near the bottom because it was close to the steel reactor head..
But it worked fairly well.

So - use your half and half, it's good first approximation. Our voltage went from roughly 8 to 15.5 volts.
I believe to calculate it exactly requires finite element-like analysis where the actual geometry is modeled.

Rest of that anecdote:
The system was temperature sensitive and the effect moved the wrong direction to be temperature coefficient of resistivity of the copper wire.. Took us a long time to figure out why.
In my calculations i'd used 400 for permeability of the shaft because that was best estimate i could get for that stainless alloy.
My measurements showed more like 25. What's up with that? Why the low permeability? Iron is iron.
Oscilloscope showed flux and excitation current ALMOST 90 degrees out of phase. Clearly there was another current encircling that iron.
Hmmmm. Eddy currents in iron by Lenz's law oppose the change in flux...
Resistivity of stainless steel is pretty high and goes up with temperature,
and that was the only physical effect that agreed with our observed temperature sensitivity.
So - we ascribed the temperature sensitivity to eddy currents making effective permeability a function of temperature, not to mention quite a bit less than expectedPoint of that digression - magnetics is "squishy" because it's fields and you need a little different thought process for fields than for circuits where everything is constrained to the conductors.
Time and temperature don't show up in textbook flux equations , and magnetic engineers have developed their own shorthand and units like v/nω So it can be daunting.
Clearly I'm no expert . I can only make approximate calculations and have to adjust them by measurement.
I posted an oscilloscope trace of one of those coil stack experiments here:, post # 14.
https://www.physicsforums.com/threads/response-time-of-a-magnetic-circuit-and-its-elements.784099/
You might enjoy that thread.

I feel like I'm bumbling. Your math is doubtless superior to mine, so i only hope to help you visualize what's physically going on.

Now - what's next ? this is good for my 'thinker'. And i enjoy the nostalgia.

old jim

ps if you get REALLY interested, find a copy of "Ferromagnetism" by Bozorth. He's the source.

 

[tim9000]

This is a forum where you can jot down your memories for future generations to stumble on. I enjoyed your anecdotes.

If i put a shorted turn around one of the outside legs the flux shifted over to the other outside leg to complete its loop. My plan was to saw an air gap in one leg and make a welder...

Do you mean no flux would travel through the leg with a shorted coil around it? This is an interesting notion, do you think you could draw a crude picture, what was your idea behind how it would be used as a welder?

Perhaps my conflict is bet illustrated with a fake example:
u = 1.2 (some made up Amophorous metal, for numerical simplicity)
N = 100
A = 0.1 meters squared
Max V = 1000 V (60 Hz as you are accustom)
so Omega w = 2pi.60
I = 10 A
Mag Len l = 1m

B = u*N*I / len = 1.2*100*10 / 1 = 1200

max B = max V / (N.A.w) = 1000 / (100*0.1*2pi*60) = 0.265
So I'd have to lower the area heaps? Likewise, if I was to use the flux equation you outlined: Φ = V/N*w = 0.0265
but also Φ = u*N*I*A / len = 120
So which Flux do I go with? There must be some simple inconcistancy I'm making but not realising. So I must disagree, my maths is not superior to yours, in this instance least of all.

How was temperature having such a huge effect on the permiability of your reactor? (I thought you were going to say there was a breakdown of lamination insulation and that was causing such large eddy currents or something) Why was it not forseen? What did you do about it?

Thanks Jim!

 

[Jony130]

I'm not a expert in magnetism, but you forget about μo - permeability of a vacuum 4Π 10 ^-7 H/m. And also your coil has inductance equal to:
L = (μμoN^2A)/l = 1.508mH and reactance for 60Hz XL = 2ΠFL = 0.5685Ω; So the current is equal to I = 1000V/0.5685Ω = 1759A (not 10A as you assume). And finally we can find a flux density
B = u*uo*N*I / len = 0.2653T or B = V / (N.A.w) = 0.2653T
Do you have any more questions/doubts ??

 

[jim hardy]

I had great difficulty editing this post to fix arithmetic and grammar errors .
System for a while refused to acknowledge "insert quotes" or even "edit" buttons... at one point i had two versions of it up ...

it looks okay now, but if you notice anything's changed , well, it probably has.

...........................

Do you mean no flux would travel through the leg with a shorted coil around it? This is an interesting notion, do you think you could draw a crude picture, what was your idea behind how it would be used as a welder?

I just spent an hour with Paint trying to draw. As usual Microsoft drove me to my knees.

It looked just about like this before i cut off the windings. Weighed probably three hundred pounds.

I was left with a three legged core. I then wound about sixty turns on center leg.
So use this schematic but the only winding present is P2, say 60 turns on center leg.

Flux enough to make 2 volts per turn flows ( let us say )UP throuh center leg (of course it's alternating but we need a mental image).
It splits , dividing between the outer legs and returns through them. It'll divide between those legs in inverse proportion to their respective reluctances, of course, which were balanced close as i could measure, i saw 1 volt per turn in each leg.

[So i just now tried in paint to draw 3 arrows representing that , the outer ones pointing down half as big as the center one pointing up. Apologies for my awkwardness]
Next i took a couple feet of of big wire and wrapped it around the right hand leg, touched the ends together rather expecting a big spark but got only a miniscule one.
The shorted turn made a MMF that opposed changing flux, and quite successfully. That's because the flux could return through the left leg.

In a normal transformer there'd be no alternate return path for flux , so the shorted turn would cancel center leg's MMF allowing my variac to push in more amps ... that's how transformers work when you think aboout it. MMF's oppose but the flux is constrained to the core so MMF primary equals very nearly MMF secondary, meaning NIprimary = NIsecondary and that's why current ratio follows turns ratio.

But my core was very happy to allow a really small current in that shorted turn to push all the flux over to the other leg.

Aha ! How interesting !
If i could cause flux to divide unequally between the legs i'd have a "variable" transformer ... put a big secondary on left leg and do something to make flux divide between the legs as i wanted.
I never finished the project, sadly - a move interrupted it and the core had to go (as Ben Franklin said "3 moves are as good as a fire.)

Here was the plan:
For a welder you want open circuit voltage to be high so it'll strike an arc
but when current starts to flow you want it to drop off quickly to the 20-30 volts required to maintain that arc.

Observe that the magnetic circuit is a source of MMF in the center leg, with left and right legs in parallel with it.
Left and right legs have equal reluctance.
So i planned to saw an air gap in the right leg raising its reluctance so that flux would shift to the left leg, and wind a 90 volt secondary there.
That would do the same thing as my shorted turn, make the flux move to left leg because it takes a lot of MMF to push flux through air.
Reluctance of right leg would be high because of air gap.As soon as current starts to flow in the left leg's winding , a MMF appears there.
That MMF is impressed across right leg because they're in magnetic parallel. So it begins to push flux through air gap in right leg, reducing left leg flux hence induced voltage.
That's the characteristic i needed, very poor voltage regulation.
By wrapping my welding lead around the right leg i'd be able to help or hinder that diversion of flux, providing current adjustment.

Back of the envelope calculations said about 1/4 inch airgap should do .

Sadly it was overtaken by events and never finished it.

Point of this digression is to get your brain thinking about pushing flux around through iron and air
because for me that's what i have to do - work it in my head, and make that process agree with the textbook equations.

As i said earlier that was ~1974 and i apologize for the lack of calculations in the presentation, details are just not sharp anymore.

I guess that exercise though was good - it erally planted in my brain the concept of MMF's in a transformer. My 1901 textbook describes Tesla's exuberance at figuring it out, "It is a marvelous self regulating system".

.................

So which Flux do I go with? There must be some simple inconcistancy I'm making but not realising.

I think i see your dilemma...

You see that these two equations are the same

B = u*N*I / len = 1.2*100*10 / 1 = 1200 <---------> Φ = u*N*I*A / len = 120

because the second one is just the first one with both sides multiplied by A.

Here's the disconnect:
You specified an inductor with ten volts per turn which at 60hz means.
10 = * w* Φcos(wt) ::: that's just familiar old n dphi/dt
10/377 = Φcos wt
Φ = .0265, which in your 0.1 meter^2 core is the B you calculated. That's the total flux(not flux density) to make 10 volts per turn, or 1000 volts per 100 turns at 60 hz.

Now - what current will make that flux?

You said you'll have 10 amps through that inductor. Well not at Φ = .0265 you won't. At 10 amps you'll get the other flux that you calculated.
B = u*N*I / len = 1.2*100*10 / 1 = 1200 , 1200sin(wt) for 60hz AC
And your volts at that flux will be what ?
V = ndΦ/dt , which = 120pi * 1200cos(wt) = 452400 45240 volts/turn
which is an impossible result - so what happened?
Aha - u is relative permeability, and must be multiplied by μ₀ which is 4pi X 10-7
and your value of 1.2 for u is almost air... a 100 turn air core inductor won't make much flux
so multiply by μ₀
452400 X 4piX10^-7 = .57 0.057 volts per turn , way more reasonable.
had trouble editing jh

Try to go back to the concept i had cemented into my alleged brain with my transformer core experiment,
volts per turn at given frequency is a direct measure of flux Φ, not fluxdensity B.
Flux is ∑amp turns X area/length, X physical constants μ₀ and u ,
Flux density B and MMF per unit length H are convenience terms that let you have equations not involving geometry so they work great for writing textbooks and printing datasheets.

How was temperature having such a huge effect on the permiability of your reactor? (I thought you were going to say there was a breakdown of lamination insulation and that was causing such large eddy currents or something) Why was it not forseen? What did you do about it?

Lastly - those iron rod drive shafts were not laminated at all. I can only think it was an oversight to operate them at line frequency.
We spoke to the designers and they'd never tried other frequencies or waveshapes, and seemed delighted with what we'd found.
I never did find in any literature a discussion of eddy current effects versus temperature in solenoid cores.
Somebody argued there could be other effects - Bozorth speaks of time effects in magnetizing iron , and the shaft gets strongly magnetized by the action of lifting the rods(it uses DC electromagnets) so that we're not quite centered on its B-H curve, and there's a lot of Gamma rays up there...
But i heated a shaft to ~ 200 degF and observed its behavior enough to convince myself we'd hit the nail on its head.
Eddy currents cancel flux making the inductance go down, but as the iron heats up eddy currents decrease, less flux is cancelled, so you get more flux per ampere
and inductance IS flux per ampere
so a warmer core looked like it had better u. As i said , i calculated apparent u around 25 versus the few hundred expected for stainless steel..
Apparent u is a function of both frequency and temperature, and it's not in textbook equations.
But it shows up in datasheets as different values for permeability at DC, 60 hz, 50 hz, and sometimes 400 hz. That's why you have different lamination thickness for different frequencies, and powder for radio frequencies. But i never saw a curve for temperature other than the one we empirically measured on our warehouse floor..

What did we do about it?
We learned to live with the temperature sensitivity... and improved our calibration technique.

There's a market for perhaps a dozen systems that'd get around it. As much fun as it would be, it's almost impossible to change anything in a Nuke plant.

 

[jim hardy]

Yea Jony - while i was typing.. old jim
and i had to edit an arithmetic mistalke

 

[jim hardy]

Observe that the cgs units for MMF, Gilberts and Oersteds, include that pesky 4pi.
http://www.magnetic-shield.com/pdf/how_do_you_measure_magnetic_fields_in_gauss.pdf

one Oersted = 1000/4pi amp-turns/meter , H
and one Gilbert = 10/4pi amp turns, NI

It's a too many names and nicknames to keep up with and I'm bad at names to begin with.
That's why i keep that little table handy.

Thanks again Jony.

Thanks Tim9k for the refresher. Now I'm mentally where i should have been when we started the discussion. If i learn something every day, just might know something some day.
Hope it's helped you equally.

old jim

 

[tim9000]

I'm not a expert in magnetism, but you forget about μo - permeability of a vacuum 4Π 10 ^-7 H/m. And also your coil has inductance equal to:
L = (μμoN^2A)/l = 1.508mH and reactance for 60Hz XL = 2ΠFL = 0.5685Ω; So the current is equal to I = 1000V/0.5685Ω = 1759A (not 10A as you assume). And finally we can find a flux density
B = u*uo*N*I / len = 0.2653T or B = V / (N.A.w) = 0.2653T
Do you have any more questions/doubts ??

You make a very valid point about the value of the current changing, however I was writing a defined case just for the example, as in I defined it that way. You also pointed out to me that I should have been more clear in my definition, I was giving the actual permiability, not the relative permiability like you interpretted, for like Metglas or some such core.

Oh Jim! That's dedication, I'm so sorry you spent an hour in Paint! I feel terrible.
I should have written that u was actual permiability, not relative, like for a Metglas.

So you were (wanting to) using the left Secondary as for doing the wealding and the right leg with the air gap to regulate the flux in it?

I think i see your dilemma...

You see that these two equations are the same

So I was right, there is a mutual exclusion in that:
'I need to define either voltage or current, otherwise I'm going to get an inconcistancy in flux'?

And to have so much flux through this (u_r.u_o = 1.2) such a big area (0.1 m^2) would require an impossible V/turn? InterestingI know that having losses in eddy currents cause heat, but the point you raise about having external heat reducing eddy currents will increase flux (and thus voltage, sounds good, maybe improve efficiency?) any problems with external heating within reason?

Thank again for all the detailed replies!

 

[jim hardy]

And to have so much flux through this (ur.uo = 1.2) such a big area (0.1 m^2) would require? produce? an impossible V/turn? Interesting

You're getting mighty close ! Probably you have it... just in case.. which is better verb to use? Require, or Produce ?

I'd state it thus:
(recall 120pi=377 , from slide rule days - saves one motion)
you used B = 1200
1200 Tesla over area 0.1m^2 = 120 Webers ,
and a single turn enclosing AC flux flux of 120sin(377t)Webers will have induced in it voltage(dflux/dt) of 377 X 120cos(377t) = 45,240 volts .
That's a LOT of volts per turn, and it takes a lot of current to push that much flux through air. That's such an improbable number it triggers a "Say What?" response.I used to carry around the plant a 0.1m^2 coil with ten turns hooked to a battery powered oscilloscope looking for stray fields. . A few feet away from the main generator conductors i could get around 3 volts as best i recall.
3volts in 10 turns is 0.3 volts per turn,

so 0.3 = 377 X Flux,
flux = 0.3/377 = 0.0008 Webers , in 0.1m^2
so B = 0.008 Tesla
That's in air, a few feet from a busbar carrying 20 kiloamps.

So when i saw B = 1200 Tesla in a core that's almost air, u only 1.2, i made same observation as Joni: something's impractical about our assumptions. Air should be in the milli or micro Teslas with only ten amps. Not to mention most steel saturates around 1.5 to 2 Tesla.

Your math was fine. Your thought experiment did the job. Thanks for the effort !

I know that having losses in eddy currents cause heat, but the point you raise about having external heat reducing eddy currents will increase flux (and thus voltage, sounds good, maybe improve efficiency?) any problems with external heating within reason?

I never thought about efficiency..
Good transformer cores are laminated to reduce eddy currents.
Our problem is we need the inductance to be very linear with core insertion, and repeatable. Rod position is basically measured by that inductance...
Efficiency isn't an issue for us there because we're not moving power with this inductor, instead trying to precisely locate where is its core.
It sits atop the reactor head where ambient is maybe 150 degf, and the steel reactor head itself is 600degF inside & probably 400F outside.
So - external heating WAS our problem. It affects measured inductance as I've described. Temperature up there on top of head follows reactor power.

In any practical inductor you'll have a better core that's less temperature sensitive due to either laminations or an air gap.

Congratulations on your progress ! I had fun too.

old jim

old jim

 

[tim9000]

Ha, oh dear, what I mean is I had 'u' correct in the first place, it's not like an air core, I should have specified because the permiability is SO HIGH (1.2) I should have specified that it wasn't the relative permiability. I thought an Amophorous metal like metglas would work well in the example but it just caused confusion.

So if there was more flux due to the increased temperature, did that mean the permiability was increasing, and your inductance was going up? (nonlinearly)

Finally, so was I correct interpreting you that one can't set V and I and use these formulas:
B*A = V / N*w
or B = u.N.I / l
at the same time because they both produce different amounts of flux? Hense you must either choose current or voltage? Because what I think you're getting at is that I've been looking at those equations like how I just wrote, but the way I should think about them is:
B = u.N.I / l
Thus V = B*A*N*w (for the length of all the turns)
and not B= V / A*N*w
as I originally thought?

Good talking with you

 

[dlgoff]

I wish there was a "Like" button for this whole thread.

 

[jim hardy]

Ha, what I mean is I had 'u' correct, it's not like an air core, I should have specified because the permiability is SO HIGH (1.2) I should have specified that it wasn't the relative permiability. I thought an Amophorous metal like metglas would work well in the example but it just caused confusion.

Ahhh i see ... i did get confused... Steels i know of won't carry 1200 Teslas they'll saturate before 2T, so i assumed you'd made a mistake there. Sorry for doubting you.

Finally, so was I correct interpreting you that one can't set V and I and use these formulas:
B*A = V / N*w
or B = u.N.I / l
at the same time because they both produce different amounts of flux? Hense you must either choose current or voltage?

You GOT it ! Probably you had it from the start. I have to work from mental models and i envy people who can work straight from the equations.
When you pick volts per turn you've defined flux
so pick an area for core that'll support that flux without saturating,
B is flux/area
then pick amp-turns you want to produce that B and you've defined reluctance of your core, which is set by its u and length and airgaps, and if you have to reach back and tweak your area - well, so it goes !.@ dlgoff - Thanks for the kind words ! You are always supportive and it's appreciated..

 

[jim hardy]

Finally, so was I correct interpreting you that one can't set V and I and use these formulas:

Because what I think you're getting at is that I've been looking at those equations like how I just wrote, but the way I should think about them is:
B = u.N.I / l
Thus V = B*A*N*w (for the length of all the turns)
and not B= V / A*N*w
as I originally thought?

Absolutely.
why didn't i think of that ? [ Big Sheepish Grin icon...]

though I'm not quite sure what you mean by " (for the length of all the turns) " . Length is in your B term..

I knew it was a simple disconnect... just couldn't pin it .
Amazing , isn't it, how difficult it is to put ideas into exact words?
Lavoisier said "Science is but language well arranged."

I had a good time. Thanks !

 

[tim9000]

Absolutely.
why didn't i think of that ? [ Big Sheepish Grin icon...]

though I'm not quite sure what you mean by " (for the length of all the turns) " . Length is in your B term..

I knew it was a simple disconnect... just couldn't pin it .

I had a good time. Thanks !

By length of turns (that was a stupid way of writing it) I just meant the voltge per whole lot rather than V/turn.

No, thank you! appreciate the great dialogue mate.

 

[jim hardy]

Great !

say --- have you a link to that Metglas core material? All i could find was their brazing compounds.

 

[tim9000]

Sorry no, only Wiki, which according to that has a permiability of 1.26 (on the Permiability page)
http://en.wikipedia.org/wiki/Metglas
No doubt it can't handle over 1200 T either, I hadn't/haven't done any real research as of yet. Just a point of interest.

 

[jim hardy]

Cool ! Found a couple links in Wiki references..

http://metglas.com/products/magnetic_materials/2714a.asp
http://metglas.com/assets/pdf/2714a.pdf

http://www.elnamagnetics.com/wp-content/uploads/library/Metglas/2605SA1.pdf

amazing stuff... relative permeability around a million !
Saturates ~ half Tesla they say...

 

[tim9000]

Cool ! Found a couple links in Wiki references..

http://metglas.com/products/magnetic_materials/2714a.asp
http://metglas.com/assets/pdf/2714a.pdf

http://www.elnamagnetics.com/wp-content/uploads/library/Metglas/2605SA1.pdf

amazing stuff... relative permeability around a million !
Saturates ~ half Tesla they say...

Ah, there you go, can't have your cake and eat it too.
I lookforward to going through those .pdfs more thoroughly, how great is the internet :p