Destructive interference in Unpolarised light

[JohnHon]

Destructive interference is excellently demonstrated in Young's double slit experiment, where dark regions are formed due the waves being out of phase. However, what really confuses me is that unpolarised light has intensity.

Assuming we had perfectly unpolarised light, as in where the electric field vectors are equal in magnitude in every direction at a single point in space (basically different waves destructively interfering), how does that beam of light produce intensity? In fact for this perfectly unpolarised light beam, shouldn’t we detect nothing, as there is never a NET electric field and thus no intensity?

So can someone explain how somehow in the double slit experiment there is 0 intensity in destructive interference yet unpolarised light DOES have intensity?

 

[RPinPA]

You're also assuming completely coherent light, so that each wave in each plane reaches the same intensity at the same instant. And you're assuming monochromatic light, so all the phase relationships are constant. Neither of those things is true with an ordinary light source. When waves add incoherently, their energies add.

 

[Ibix]

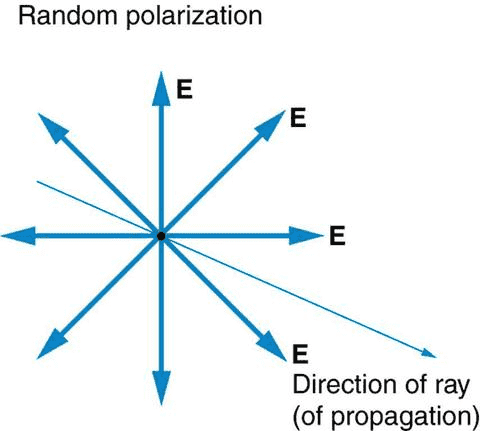
Assuming we had perfectly unpolarised light, as in where the electric field vectors are equal in magnitude in every direction at a single point in space

Where did you find this definition of unpolarised light? It doesn't seem right to me. I'd agree that, over time, you will find the electric field vector at a given point does at some time point in every available direction, but the direction at a point at a single instant is well-defined. It just doesn't tell you anything about the direction at any other point, or at any other time.

 

[Cryo]

Unpolarized light simply means that polarization of light changes faster than the detection capability of your apparatus. It also means that polarization changes in a random fashion. But polarization at any instant is well-defined. When you start doing Young's interference you have (e.g.) two copies of electric field that you guided along different paths. Let's say that electric field on the screen is given by:

$\mathbf{E(t)}=\mathbf{E}_1 (t) + \mathbf{E}_2 (t)$

Where $\mathbf{E}_{1,2}$ are the electric fields guided along different paths. Let's simplify and say that the only difference between them is that $\mathbf{E}_{1}=\mathbf{E}_0 (t-t_1)$ and $\mathbf{E}_{2}=\mathbf{E}_0 (t-t_2)$, where $\mathbf{E}_0$ is the original source. So we are saying the two interfering fields are simply routed through two delay lines.

If the source is random, there is usually some sort of coherence time $\tau$ within which the randomness of the source is negligible. So as long as $t_2-t_1<\tau$ you will see interference fringes. Note, than one often talks of coherence length $L=c \tau$, where $c$ is the speed of light.

 

[tech99]

Interestingly, if we have a pure CW source we cannot obtain unpolarised radiation from it. A classical source of unpolarised light consists of two orthogonal antennas each driven by a noise generator.