SUMMARY
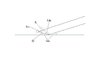
The discussion centers on calculating the angle above the horizon at which a star emitting 21cm wavelength microwave radiation first reaches maximum intensity as detected by a microwave detector positioned 0.5m above a lake. The key to solving this problem lies in understanding the path length difference between the direct wave from the star and the reflected wave off the lake, which must be an integer multiple of the wavelength for constructive interference. The final equation derived is mλ = sin(θ), where m is an integer and θ is the angle of reflection, leading to the conclusion that the first maximum occurs at approximately θ = 0.21 radians.
PREREQUISITES
- Understanding of wave interference principles
- Familiarity with trigonometric functions and their applications in physics
- Knowledge of microwave radiation properties, specifically wavelength
- Ability to interpret and construct geometric diagrams for wave paths
NEXT STEPS
- Study the principles of constructive and destructive interference in wave physics
- Learn about the applications of trigonometry in solving physics problems
- Explore the properties of microwave radiation and its detection methods
- Review geometric optics, particularly reflection and refraction principles
USEFUL FOR
Students and educators in physics, particularly those focusing on wave mechanics and interference, as well as anyone involved in experimental astrophysics or microwave detection technologies.