Determination of a magnetic field with kinematics

[scoldham]

Homework Statement

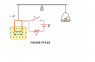
The figure attached illustrates a setup that can be used to measure the magnetic field. A rectangular coil of wire contains N turns and has a width w. The coil is attached to the one arm of a balance and is suspended between the poles of a magnet. the field is uniform and perpendicular to the plane of the coil. The system is first balanced when the current in the coil is zero. When the switch is closed and the coil carries a current I, a mass m must be added to the right side to balance the system. Suppose the coil has 50 turn and width of 5.00 cm. When the switch is closed, the coil carries a current of 0.3 A, and a mass of 20 g must be added to the right side to balance the system. What is the magnitude of the magnetic field?

Homework Equations

$$F = I B l$$

$$F = m a$$

The Attempt at a Solution

Setting up a force balance and working the above equations has gotten me to this point:

$$B = \frac{m g}{I l}$$

Thus, the magnetic field. However, I'm not sure where the "50 turns" comes into play... plus there's a resistor int he diagram. I cannot help but to think these come into play some how that I am missing...

Do the turns generate a back emf? If so, how does that affect the B field... does it affect it all?

 

[Stonebridge]

You are correct that the force on the wire is BIL (L=w in this example)
But that would be for a single wire. In a coil of 50 turns, each separate strand of the wire will experience this force. I don't think the resistance in the circuit has any relevance to this question.

 

[scoldham]

The only relationship I can find where coils come into play is with the flux and emf.

$$\epsilon = -N \frac{d \Phi_B}{d t}$$

Even working on that equation a little doesn't give me any good relationship defining how N affects the B field. Is there an equation I'm missing?

 

[Stonebridge]

The force in question acts downwards on the lower horizontal side of the square coil. As you said in you 1st post, and I confirmed, the force on a single wire of length L in a field B is F=BIL
That's BIw in this question where I and w are given.
However, there are 50 wires in the coil and each one experiences the same force.
So the total downwards force on the lower side of the coil is 50 times BIw.
There is no force on the upper side of the coil because it is not in the field. There is no downward or upward force on the vertical sides of the coil because the current in them is such that the force is to the left or right.
When the system is balanced, there is no induced emf because there is no motion.
So the mg of the mass is balanced by the downward force on the lower side of the coil.

 

[scoldham]

So it is as simple as:

$$B = \frac{mg}{N I l}$$

?

 

[Stonebridge]

So it is as simple as:

$$B = \frac{mg}{N I l}$$

?

It appears so. The whole "coil" thing is a bit of a sidetrack and confuses the issue. The question is just about the force on that lower side of the square. The diagram gives it away, as the coil is not completely in the magnetic field. It it were, the upward force on the upper side, would balance the downward force on the lower side and absolutly nothing would happen.

 

[scoldham]

Great! I'll give this a shot and hope for the best.

Thank you for your assistance.