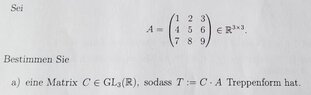Determine a matrix C such that T = CA has echelon form

[mathmari]

Hey!

Let $$A=\begin{pmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{pmatrix}\in \mathbb{R}^{3\times 3}$$

I want to determine a matrix $C\in GL_3(\mathbb{R})$ such that $T:=C\cdot A$ has echelon form. Performing an elementary row operation is equivalent to multiplying an invertible matrix, right? (Wondering)

So do we apply the Gauss algorithm at $[A \ \mid \ I_3]$, and bring $A$ into echelon form, then the $3\times 3$-matrix that we get on the right side is the matrix $C$ that we are looking for, i.e. we get $[T \ \mid \ C]$ ?

I mean the following:
\begin{equation*}\begin{pmatrix}1 & 2 & 3 & 1 & 0 & 0 \\ 4 & 5 & 6 & 0 & 1 & 0\\ 7 & 8 & 9 & 0 & 0 & 1\end{pmatrix}\longrightarrow \begin{pmatrix}1 & 2 & 3 & 1 & 0 & 0 \\ 0 & -3 & -6 & -4 & 1 & 0\\ 0 & -6 & -12 & -7 & 0 & 1\end{pmatrix}\longrightarrow \begin{pmatrix}1 & 2 & 3 & 1 & 0 & 0 \\ 0 & -3 & -6 & -4 & 1 & 0\\ 0 & 0 & 0 & 1 & -2 & 1\end{pmatrix}\end{equation*}
(Wondering)

At the proposed solution they continue the Gauss algorithm and they get the following:
\begin{equation*}\begin{pmatrix}1 & 2 & 3 & 1 & 0 & 0 \\ 4 & 5 & 6 & 0 & 1 & 0\\ 7 & 8 & 9 & 0 & 0 & 1\end{pmatrix}\longrightarrow \begin{pmatrix}1 & 2 & 3 & 1 & 0 & 0 \\ 0 & -3 & -6 & -4 & 1 & 0\\ 0 & -6 & -12 & -7 & 0 & 1\end{pmatrix}\longrightarrow \begin{pmatrix}1 & 2 & 3 & 1 & 0 & 0 \\ 0 & 1 & 2 & \frac{4}{3} & -\frac{1}{3} & 0\\ 0 & 0 & 0 & 1 & -2 & 1\end{pmatrix} \longrightarrow \begin{pmatrix}1 & 0 & -1 & -\frac{5}{3} & \frac{2}{3} & 0 \\ 0 & 1 & 2 & \frac{4}{3} & -\frac{1}{3} & 0\\ 0 & 0 & 0 & 1 & -2 & 1\end{pmatrix}\end{equation*} Why do they change also the first two rows although we already have the echelon form? Would it be wrong to stop the algrithm as I did it? I mean is it wrong to consider the matrices \begin{equation*}T=\begin{pmatrix}1 & 2 & 3 \\ 0 & -3 & -6 \\ 0 & 0 & 0 \end{pmatrix} \ \text{ and } \ C=\begin{pmatrix}1 & 0 & 0 \\ -4 & 1 & 0 \\ 1 & -2 & 1\end{pmatrix}\end{equation*} ? (Wondering)

 

[I like Serena]

Hey mathmari!

There's a difference between Row Echelon Form (REF) and Reduced Row Echelon Form (RREF).
RREF means that:

• It is in row echelon form.
• Every leading coefficient is 1.
• The leading coefficient is the only nonzero entry in its column.

(Thinking)

 

[mathmari]

There's a difference between Row Echelon Form (REF) and Reduced Row Echelon Form (RREF).
RREF means that:

• It is in row echelon form.
• Every leading coefficient is 1.
• The leading coefficient is the only nonzero entry in its column.

(Thinking)

At the exercise statement it is asked for Row Echelon Form:

View attachment 8386

So is the proposed solution for the case of Reduced Row Echelon Form and in the case of Row Echelon Form we could also do what I did? (Wondering)

 

[I like Serena]

At the exercise statement it is asked for Row Echelon Form:



So is the proposed solution for the case of Reduced Row Echelon Form and in the case of Row Echelon Form we could also do what I did? (Wondering)

Yep.
It looks as if the proposed solution went 'over the top'. (Emo)

 

[mathmari]

Yep.
It looks as if the proposed solution went 'over the top'. (Emo)

Ok! Thank you! (Yes)