Determine Force on 6ft Door Due to Water & Air Pressure

[MiMiCiCi22]

Homework Statement

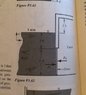
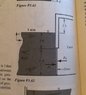
Determine the total force and its direction (left or right) due to water and air pressure in the surface shown in Fig. P3.62 (lb f). The door is hinged at the top and is 6 feet wide. See attached image.

Homework Equations

Fp (force of pressure) = specific weight of fluid * depth to center of gravity * Area
P=F/A
Pg (gauge pressure) = specific weight of fluid * depth
Specific weight of water = 62.4 lb/ft^2
lbf = pounds of force

The Attempt at a Solution

I first tried to find the force of pressure from the water acting on the side of the door...
Fp = (62.4 lbf/ft^2)*(3ft+2.5ft)*(5ft)*(6ft)
Fp = 10296 lbf
I then thought that if I added the force of pressure from the water acting on the side of the door to the force of pressure from the air acting on the side of the door, I would be able to find the total force. I first converted 2 atm to lbf/ft^2...
2 atm * (0.0209 lb/ft^3)/(9.869x10^-3 atm) = 4235.48 lbf/ft^2
I then tried to find force using this pressure...
F = PA = (4235.48 lbf/ft^2)*(5ft)*(6ft)
At this point, my professor told me that I was solving it wrong.

 

[TSny]

Note that at the top of the water there is atmospheric pressure of 1 atm.

(Welcome to PF!)

 

[MiMiCiCi22]

So how do I take the atmospheric pressure into account? What would this do to my calculations?

 

[TSny]

How do you find the pressure at a point in the water at a depth h?

 

[MiMiCiCi22]

So I would need to use the Equation P=Pa+(specific gravity of water)*(h) ?

 

[TSny]

So I would need to use the Equation P=Pa+(specific gravity of water)*(h) ?

Yes [with "specific gravity" replaced by "specific weight"]

 

[MiMiCiCi22]

So I found the pressure for the water side of the door using the equation mentioned earlier. I then converted it to force using the equation F=PA. For the side with air, I converted 2 atm to lb f. I then used F=PA to convert this pressure to force. I'm currently getting a net force of 73829 acting to the left, however the correct answer is that there should be -53.184 lb f acting to the right. I'm confused as to where I may have made a mistake.

 

[TSny]

Please show the details of your calculation for the force due to the water.