Determine the tension in the two strings

[BunDa4Th]

Three objects are connected by light strings as shown in Figure P4.62. The string connecting the m1 = 6.00 kg mass and the m2 = 4.80 kg mass passes over a light frictionless pulley.

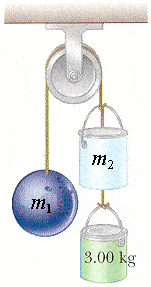
(b) Determine the tension in the two strings.
string between m2 and the 3.00 kg mass

I was able to do the first two part but this one is just troubling me and I am confuse. acceleration is 1.28 m/s^2

a = m2g + 3g - m1g / m1 + m2 + 3

and the tension between m1 and m2 is 66.48

T - m1g = m1a

but i can't seem to get m2 and the 3kg mass. this is what i tried

4.8(9.8) - 3(9.8) = 17.64 N

T - 17.64 = 7.8(1.28) = 27.624 which is incorrect. I don't know what I am doing wrong or where to start.

 

[berkeman]

You are mixing units, and that is part of your problem. a = m2g makes no sense.

Please re-write the force equations for each string, with correct units, and I think you will get it right.

 

[BunDa4Th]

what i did was T - m1g = m1a and T - m2g + 3g = (m2 + 3)a

then i solve for T for equation 1 to plug into equation two. I input the numbers and solve for a which is equal to 1.28.

a = (4.8(9.8) + 3(9.8)) / (6+4.6+3)
a = 1.28 with a solve i can solve for tension string between m1 and m2. which is T - m1(g) = m1(a)
T - 58.8 = 6(1.28) T = 66.48 N

I somewhat understand what i did there from reading the book but it didnt explain anything about if there was another add on to it. I am not sure if i did set up the equation correctly.

 

[berkeman]

You may be on the right track, but keep track of the sign of a. It should be opposite for the left and right sides. Sorry, I've got to bail for the night.