Determining the Moment of Inertia about an angle θ to the x axis

[pranjal verma]

Homework Statement

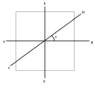
Let I be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides.CD is a line in the plane that passes through the centre of the plate and makes an angle θ with the axis AB as shown in figure. The moment of inertia
of the plate about the axis CD is equal to

Relevant Equations

I[SUB]z[/SUB]= I[SUB]x[/SUB] + I[SUB]y[/SUB](Perpendicular Axis theorem)

• I thought about solving it using components of I_AB but since it is a scalar quantity it doesn't seems to be correct .
• I don't think Perpendicular Axis theorem will work as required Inertia is in the same plane.

 

[TSny]

I don't think Perpendicular Axis theorem will work as required Inertia is in the same plane.

This theorem might be useful. Consider an axis GH that lies in the plane of the square, passes through the center, and is perpendicular to CD.

 

[pranjal verma]

This theorem might be useful. Consider an axis GH that lies in the plane of the square, passes through the center, and is perpendicular to CD.

Thank you very much sir for helping me.