Sudesh
- 9
- 0
Hi,
Could someone please help me with this.
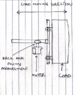
I need to move an object which weighs 300 g horizontally, which is linked to a linear actuator consisting of rack and pinion arrangement which is driven by a servo motor. The speed at which the object should move is 3 m/s and the distance is 0.5 m.
How can I determine what Torque is required to move the object?
Could someone please help me with this.
I need to move an object which weighs 300 g horizontally, which is linked to a linear actuator consisting of rack and pinion arrangement which is driven by a servo motor. The speed at which the object should move is 3 m/s and the distance is 0.5 m.
How can I determine what Torque is required to move the object?