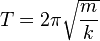Difference between Time periods

Thread starter XuFyaN
Start date Mar 20, 2010
Tags

Difference Time

Click For Summary

SUMMARY

The time period of a Simple Pendulum is directly dependent on its length, while the time period of Simple Harmonic Motion (S.H.M) is influenced by mass. Additionally, the time period of S.H.M remains unaffected by the amplitude of oscillation and the acceleration due to gravity. The derivation of the pendulum's time period is valid for small amplitude oscillations, highlighting a key distinction in their operational parameters.

PREREQUISITES

Understanding of oscillatory motion
Familiarity with the principles of pendulums
Basic knowledge of Simple Harmonic Motion (S.H.M)
Concept of amplitude in oscillations

NEXT STEPS

Research the mathematical derivation of the time period for Simple Pendulums
Explore the characteristics of Simple Harmonic Motion (S.H.M)
Study the effects of mass and length on oscillation periods
Examine the impact of amplitude on different types of oscillatory systems

USEFUL FOR

Physics students, educators, and anyone interested in the principles of oscillatory motion and their applications in mechanics.

Mar 20, 2010

XuFyaN

What is the difference between the time period of Simple Pendulum and Time period of S.H.M

i.e

and

time period of Simple Pendulum depend on length while Time period of S.H.M depend on mass , what will be the other differences?

Physics news on Phys.org

Mar 20, 2010

rl.bhat

Homework Helper

Time period of SMH does not depend on the amplitude of the oscillation and acceleration due to gravity.
Time period of pendulum is derived for the small amplitude.

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?

View full post »