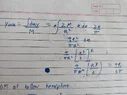SUMMARY
The discussion focuses on the methodology for calculating the center of mass of a hollow hemisphere using infinitesimal elements. The participant initially attempted to derive the formula for a half-disc but encountered difficulties when transitioning to the hollow hemisphere. Key equations referenced include equation (1), which defines the y-coordinate of an infinitesimal mass element (dm) as a semi-circle with width dx and radius x, and equation (2), which requires clarification on the y-coordinate used. The conversation emphasizes the importance of clear mathematical notation and the use of TeX for better readability.
PREREQUISITES
- Understanding of calculus, particularly integration techniques.
- Familiarity with the concept of center of mass in physics.
- Knowledge of geometric shapes, specifically hemispheres and discs.
- Proficiency in LaTeX for mathematical typesetting.
NEXT STEPS
- Research the derivation of the center of mass for various geometric shapes, focusing on hollow hemispheres.
- Learn about the application of infinitesimal calculus in physics problems.
- Explore the use of LaTeX for presenting mathematical equations clearly.
- Study the differences in calculating center of mass for solid versus hollow objects.
USEFUL FOR
Students and educators in physics and mathematics, particularly those dealing with mechanics and geometric applications, will benefit from this discussion.