Differential operator, inverse thereof

[member 428835]

Hi PF!

I'm reviewing a text and the author writes

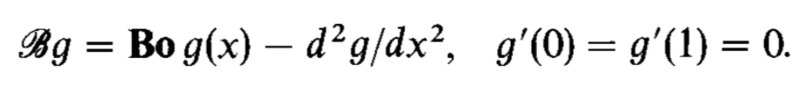
where $g$ is an arbitrary function and $B$ is a differential operator. $Bo$ is a parameter. Then the author states the inverse of $B$ is

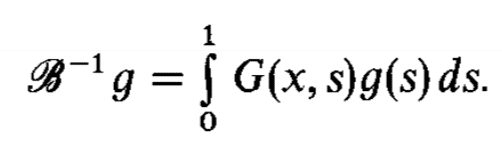
where $G$ is the Green's function of $B$. Can someone explain how we know this?

 

[Orodruin]

The Green's function in this case is defined as the function for which
$$
\mathscr B G(x,s) = \delta(x-s)
$$
and $G(0,s) = G(1,s) = 0$. Hence
$$
\mathscr B \mathscr B^{-1} g = \int_0^1 \mathscr B G(x,s) g(s) ds = \int_0^1 \delta(x-s) g(s) ds = g(x)
$$
and $\mathscr B \mathscr B^{-1}$ is the identity operator.

 

[member 428835]

Thanks!

 

[member 428835]

The Green's function in this case is defined as the function for which
$$
\mathscr B G(x,s) = \delta(x-s)
$$
and $G(0,s) = G(1,s) = 0$.

Can you explain where you got the BC from? Is is always the case for Greens functions that the boundaries be zero? If so, would you mind explaining why?

 

[Orodruin]

Typically you want the Green's function to satisfy homogeneous boundary conditions of the same type as the boundary conditions of your differential equation (even if the differential equation has inhomogeneous boundary conditions). This means that you can built the inhomogeneity in the differential equation from the Green's function without affecting the boundary conditions. You are then left with solving the homogeneous differential equation if you have inhomogeneous boundary conditions. This can also be done using the Green's function, but is yet another step and you anyway have homogeneous boundary conditions.

Exercise: Check that letting the Green's function satisfy homogeneous boundary conditions lead to $g$ satisfying homogeneous boundary conditions.

 

[Orodruin]

Oh, sorry. I misread the original post. You should use Neumann conditions instead. Note that this will be incompatible with the case $B_0 = 0$ though. Anyway, the boundary conditions are not the main issue for your question.

 

[member 428835]

Exercise: Check that letting the Green's function satisfy homogeneous boundary conditions lead to $g$ satisfying homogeneous boundary conditions.

Okay, so to find the Green's function I would take, as you said, $BG(x,s) = \delta(x-s)$. For simplicity, let's let $Bo = 0$. Then we have $d^2_x G = \delta(x-s)$ subject to $G(x=0)=0$ and $G(x=1)=0$. To satisfy BC without a trivial solution, make the Green's function a continuous, but not necessarily every differentiable, function. Then we have a left and right (with respect to $s \in (0,1)$) solution to $d^2_x G = 0$ taking the form $G_L = a x$ and $G_R = b (1-x)$. Continuity implies $G_L(x=s) = G_R(x=s)$ and a final condition requires $\int_{x-}^{x+} G'' = 1$. Then the solutions I get are $$G_L = (1-s)x\\ G_R = s(1-x).$$ So far so good?

 

[member 428835]

Oh, sorry. I misread the original post. You should use Neumann conditions instead. Note that this will be incompatible with the case $B_0 = 0$ though. Anyway, the boundary conditions are not the main issue for your question.

Sorry, I just saw this after responding to your previous post. But the text also gives

and I'm unsure how to arrive at the case where $Bo = 0$. Any ideas?

 

[Orodruin]

But the text also gives

This does not look correct to me. For example, taking the $Bo = 0$ case, it is clear that $\partial_x^2 G = 1$, not $\delta(x-s)$.

 

[member 428835]

This does not look correct to me. For example, taking the $Bo = 0$ case, it is clear that $\partial_x^2 G = 1$, not $\delta(x-s)$.

Yea, it didn't seem like I could reproduce their work either. Would you mind looking at the two attachments? This is where the author begins discussing the $B$ operator. I'm agree (obviously) with the eigenvalues and eigenfunctions of $B$. But I am lost at the Green's functions. Does reading this snippet make anything clearer to you?

 

[member 428835]

The Green's function in this case is defined as the function for which
$$
\mathscr B G(x,s) = \delta(x-s)
$$
and $G(0,s) = G(1,s) = 0$. Hence
$$
\mathscr B \mathscr B^{-1} g = \int_0^1 \mathscr B G(x,s) g(s) ds = \int_0^1 \delta(x-s) g(s) ds = g(x)
$$
and $\mathscr B \mathscr B^{-1}$ is the identity operator.

I had a question for you Orodruin: why is the Green's function defined in the case with homogenous BCs: $G(0,s) = G(1,s) = 0$? If we're finding the inverse operator of $B$, I'm confused why there are any restrictions at all on the boundaries of $G$?

 

[Orodruin]

Because you want to solve a linear differential equation with exactly those homogeneous boundary conditions and superpositions of such Green's functions also satisfy those homogeneous boundary conditions. If you have inhomogeneous boundary conditions you still want to define the Green's function with homogeneous boundary conditions. You then write the solution as a superposition of the integral with the Green's function that will satisfy the inhomogeneity in the differential equation and a solution to the homogeneous differential equation that takes care of the inhomogeneous boundary conditions.

I discuss the general form of the Green's function solutions to a linear problem with linear boundary conditions in section 7.2.3 of my book.

 

[member 428835]

I discuss the general form of the Green's function solutions to a linear problem with linear boundary conditions in section 7.2.3 of my book.

Thanks! What's the book you're referring to? Have a title (and author, since I'm not sure of your name)?

 

[DrClaude]

Thanks! What's the book you're referring to? Have a title (and author, since I'm not sure of your name)?

https://www.amazon.com/dp/113805688X/?tag=pfamazon01-20

 

[member 428835]

Thanks!

 

[Orodruin]

https://www.amazon.com/dp/113805688X/?tag=pfamazon01-20

See also https://www.physicsforums.com/insights/the-birth-of-a-textbook/ and my avatar.

 

[member 428835]

Very interesting article. Shockingly sounds very relevant to what I do. I'll have to grab a copy (but I'm first going to check our library, maybe they've beat me to the punch).