physicsissohard
- 19
- 1
- Homework Statement
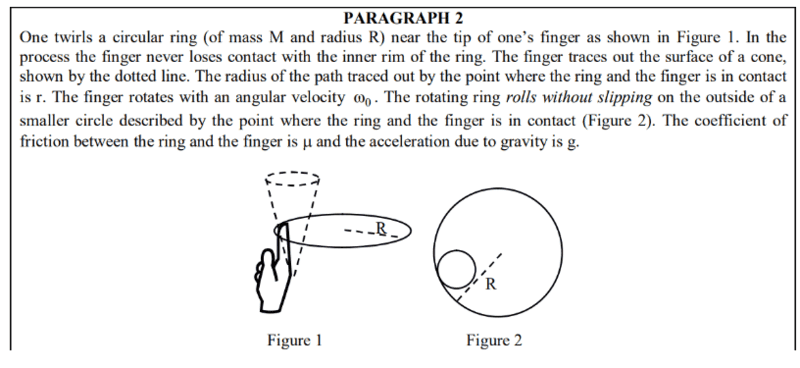
- One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1 In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity omega_o. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure-2). The coefficient of friction between the ring and the finger is u and the acceleration due to gravity is g
- Relevant Equations
- its down
This question is from the Jee Advanced 2017. This question stumped me because it was very difficult to do, the first part of the comprehension was asking for the kinetic energy of the ring.
This is what I mean.
Using the no-slip condition we can write ##\omega R-v_c=\omega_0r##. This is the no-slip condition. the relative velocity between the finger and the point of contact of the ring is ##0##. I assumed the angular velocity vector to be pointing out of the page and the finger to be moving in the counterclockwise direction, this is obvious through intuition.
Now if you draw fbd of the ring, you can come up with the equation ##N=\frac{mv^2}{x}##. Where ##N## is the normal force and ##x## is the distance between the center of mass and the IAOR(instantaneous axis of Rotation). the other equation is ##f=mg## and ##f=\mu N## where ##f## is the frictional force.
I don't know what to do with these how do they help solve the questions. This is the actual physics way to do it. All the other solutions on youtube and else where just assume by intuition(not obvious though) that the IAOR is at the center of the small circle, which basically sovles the question. Now I want proof of that, why is IAOR of this system the center of small ring. I came up with equations as shown as above but for some reason they aren't helping why?
I used the defining feature of the system to create equations, what did I miss.
This is what I mean.
Using the no-slip condition we can write ##\omega R-v_c=\omega_0r##. This is the no-slip condition. the relative velocity between the finger and the point of contact of the ring is ##0##. I assumed the angular velocity vector to be pointing out of the page and the finger to be moving in the counterclockwise direction, this is obvious through intuition.
Now if you draw fbd of the ring, you can come up with the equation ##N=\frac{mv^2}{x}##. Where ##N## is the normal force and ##x## is the distance between the center of mass and the IAOR(instantaneous axis of Rotation). the other equation is ##f=mg## and ##f=\mu N## where ##f## is the frictional force.
I don't know what to do with these how do they help solve the questions. This is the actual physics way to do it. All the other solutions on youtube and else where just assume by intuition(not obvious though) that the IAOR is at the center of the small circle, which basically sovles the question. Now I want proof of that, why is IAOR of this system the center of small ring. I came up with equations as shown as above but for some reason they aren't helping why?
I used the defining feature of the system to create equations, what did I miss.
Last edited by a moderator: