Difficult relative velocity problem

[PieOperator]

Homework Statement

A helicopter velocity relative to the ground is flying south for exactly .75hours. A wind blows and the helicopter ends up 30 Km in a southwesterly position away from her starting point. the helicopter speed relative to the ground is 50km/hour. What is the direction and the speed of the wind?

Homework Equations

Vhg + Vwg = Vha

d1 + d2 = d3

Speed x time = distance

Law of cosines
Law of sines

The Attempt at a Solution

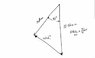
I've gotten to this point without using matrices and without using polar vector coordinates.

Two triangles seem to appear similar when there are no units...however they are not.

One triangle was formed from using just speeds.
40 km/hour = Speed of helicopter relative to air
50 km/hour = speed of helicopter relative to ground
W = speed of wind relative to the ground

Another triangle was formed from using just distances
37.5 km = distance to the south
30 km = distance to the southwest

D = distance in the direction of the wind

There is a multiple of .75 hours from speed of wind to the distance traveled in direction of the wind.

The two triangles form a proportion of 4/5. THIS PROPORTIONALITY IS DIFFERENT FROM .75 !

Help

 

[Spinnor]

If the picture is right you have two lengths and an angle. See,

 

[PieOperator]

If the picture is right you have two lengths and an angle. See,

Yes! How'd you know the angle is 45 degrees??

 

[Spinnor]

You wrote,

"A wind blows and the helicopter ends up 30 Km in a southwesterly position away from her starting point. "

The angle between the south and southwest directions is 45 degrees.

 

[PieOperator]

Southwesterly is not sufficient to concluding 45 degrees. There is a way to figure it out without assuming 45 degrees. I just don't know how to do it due to the weird similar triangles I get.

But the angle does turn out to be 45 degrees