SUMMARY
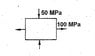
The discussion focuses on determining the normal stress acting on the plane of maximum shear stress using both analytical methods and Mohr's circle. The maximum shear stress occurs at an angle of 45 degrees relative to the maximum applied stress of 100 MPa, resulting in a calculated normal stress of 25 MPa (tensile). The participants clarify the importance of correctly identifying the signs of normal stresses, emphasizing that one stress is positive while the other is negative. The analytical approach involves using the stress tensor and unit normal vectors to derive the normal and shear stress components.
PREREQUISITES
- Understanding of stress transformations in mechanics
- Familiarity with Mohr's circle for stress analysis
- Knowledge of stress tensor representation in dyadic notation
- Proficiency in trigonometric functions and their application in engineering
NEXT STEPS
- Study the derivation of normal stress components from the stress tensor
- Learn about Mohr's circle and its applications in stress analysis
- Explore the concept of shear stress and its maximum conditions
- Investigate the implications of stress sign conventions in engineering mechanics
USEFUL FOR
Mechanical engineers, civil engineers, and students studying solid mechanics who need to understand stress transformations and their applications in structural analysis.