johnsonb.engr
- 11
- 0
Hello All
I could get some help I would greatly appreciate it.
I am trying to figure how to calculate the dissolution time of sphere undergoing constant corrosion at a rate
of corrosion.
Through a little google-fu, I found an article which gives me the solution ( http://arxiv.org/pdf/1208.5925.pdf )
but I am having trouble understanding the proof.
In this article there is a dissolving sphere
From this article we know that
the mass of the sphere is equal to dm/dt = -c*s(m) (1
and the general solution is
m(t)=mo - A*(mo^2/3)*t + (1/3)*(A^2)*(mo^(1/3))*(t^2) -1/27*(A^3)*(t^3)
or
m(t) = (a-k*t)^3
a = initial mass = (mo)^1/3
k = (A/3).
The article then gives an example where
mo = initial mass = 10 grams
p = density = 0.8 mg/mm^2
c = corrosion rate = -0.003 mg/(s*mm^2)
I am having difficulty understanding how to relate the rate of corrosion c to A.
I know that c = (dm/dt)/s(m)
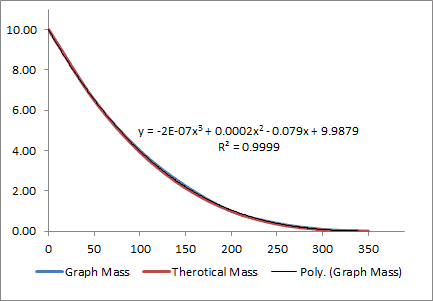
The article shows a series of graphs for Mass, Radius, SA, and Volume vs time.
I copied these graphs into excel and add used excel to find a trendline.
m(t) = -2E-07*t^3 + 0.0002*t^2 - 0.079t+ 9.9879
By plugging values into the trend line above I was able to find a solution to
A = 0.0173.
However, do not understand how to relate A to c(-0.003).
Some help would be greatly appreciated.
I could get some help I would greatly appreciate it.
I am trying to figure how to calculate the dissolution time of sphere undergoing constant corrosion at a rate
of corrosion.
Through a little google-fu, I found an article which gives me the solution ( http://arxiv.org/pdf/1208.5925.pdf )
but I am having trouble understanding the proof.
In this article there is a dissolving sphere
From this article we know that
the mass of the sphere is equal to dm/dt = -c*s(m) (1
and the general solution is
m(t)=mo - A*(mo^2/3)*t + (1/3)*(A^2)*(mo^(1/3))*(t^2) -1/27*(A^3)*(t^3)
or
m(t) = (a-k*t)^3
a = initial mass = (mo)^1/3
k = (A/3).
The article then gives an example where
mo = initial mass = 10 grams
p = density = 0.8 mg/mm^2
c = corrosion rate = -0.003 mg/(s*mm^2)
I am having difficulty understanding how to relate the rate of corrosion c to A.
I know that c = (dm/dt)/s(m)
The article shows a series of graphs for Mass, Radius, SA, and Volume vs time.
I copied these graphs into excel and add used excel to find a trendline.
m(t) = -2E-07*t^3 + 0.0002*t^2 - 0.079t+ 9.9879
By plugging values into the trend line above I was able to find a solution to
A = 0.0173.
However, do not understand how to relate A to c(-0.003).
Some help would be greatly appreciated.
