SUMMARY
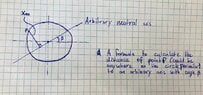
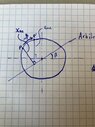
The discussion focuses on formulating an equation for the shortest distance from a point on the perimeter of a circle to an arbitrary axis, given the circle's radius R and angle θ. Participants emphasize the use of rotation matrices to determine the new coordinates after rotating the point around the origin by angle -β. Key steps include identifying the reference line equation as y=(tan β)x and deriving the perpendicular line's equation to find the intersection point, which ultimately leads to calculating the distance PQ as a function of R, θ, and β.
PREREQUISITES
- Understanding of rotation matrices
- Knowledge of trigonometry, specifically right triangles
- Familiarity with the concept of angles in standard position
- Ability to work with linear equations and their intersections
NEXT STEPS
- Study the properties of rotation matrices in 2D geometry
- Learn how to derive equations for lines and their intersections
- Explore trigonometric identities related to angles and distances
- Investigate applications of the Pythagorean Theorem in coordinate geometry
USEFUL FOR
Students and educators in mathematics, particularly those studying geometry and trigonometry, as well as anyone involved in solving problems related to distances in coordinate systems.