Divide circle into 9 areas

[Nick89]

Hi,

I was asked this question on another forum and was interested in it... It's somewhat related to what I have been doing lately so I gave it a (few) tries, but I never really worked it out...


Consider a circle with a radius of 32 units. We want to divide the area of the circle into 9 areas that have, if possible, exactly the same area. See the following image:

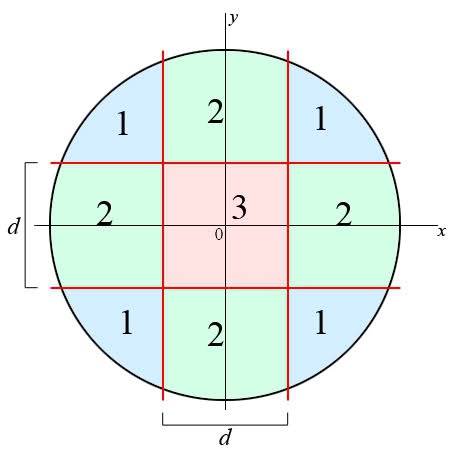
The red lines are the 'dividing lines', spaced by a distance $d$ (in the x as well as the y direction).

The areas 1 (blue) and 2 (green) and the area 3 (red) are marked with the colors. Note that there are four areas 1 and four areas 2, they should be equal in area.


The question is how to find the distance $d$ that will yield the optimal result (if possible, that all areas are equal).



The first thing I thought about (but which doesn't seem to be working, see later) is simply to do the following:

We know the area of the complete circle: $$A_{tot} = \pi 32^2$$
Therefore, if the 9 areas are to be divided in equal areas, the area of one the subareas will be: $$A_{sub} = \frac{ \pi 32^2}{9}$$
We also know the area $A_3$ since it's just a square: $$A_3 = d^2$$
Therefore: $$d = \sqrt{ \frac{ \pi 32^2}{9}}$$.


I tried to graph it and it seemed alright to the eye, but I wanted to be sure, so I went on...



The following way I could think of was to calculate the subareas seperately using integrals and then looking for a $d$ that would minimize their deviation.

I came up with the following area's; $A_1$ is calculated from the top-right area1 and $A_2$ is calculated from the rightmost area2.

$$A_1 = \int_\frac{d}{2}^b \left( \sqrt{ 1024-x^2} - \frac{d}{2} \right) \, dx$$
$$A_2 = 2 \times \left( \int_b^{32} \sqrt{1024-x^2} \, dx \right) + d \sqrt{1024-\frac{d^2}{4}}$$
$$A_3 = d^2$$
where the limit b is the intersection of the circle with y = d/2:
$$b = \sqrt{1024-\frac{d^2}{4}}$$


When I now plugged in the value for $d$ I found above I don't get the same result, I get a different result for each area...


So, I thought, maybe my simple solution above wasn't right.
But now I have found three areas each as a function of d. I should be able to minimize the deviation between the areas for one value of d, right? I can't see any way how to do that though... Maybe taking the absolute value of the deviation (A_1 - A_2 for example) and using solving it's derivative for 0? Even then I only minimized A_1 - A_2 and had nothing to do with A_3...


Where have I gone wrong:
1) Assuming there is a solution where all areas are equal;
2) Assuming this solution was simply to divide the total area by 9 and equaling this to d^2;
3) Calculating the areas using integrals?

I can't see any other mistakes I may have made, so I assume it must be one of the three...

Could anyone help me out here?

 

[CRGreathouse]

I would calculate the areas (with integrals as needed) as a function of d, then try to minimize
$$4(A_1-A)^2+4(A_2-A)^2+(A_3-A)^2$$ with $$A=1024\pi/9$$