I Do gravitons interact with gravitons?

[ohwilleke]

A key weakness that I see in Deur's models as alternatives to dark matter is that they only address the specific case of galaxy rotation curves. But that is not the only case in which the dark matter hypothesis comes into play in the current Lambda CDM model of our universe. As far as I can see, Deur's models give no help at all in avoiding the dark matter hypothesis in, for example, the evolution of the early universe. His model depends on gravitational properties of isolated bound systems like galaxies and does not even apply to relatively uniform matter distributions like those in the early universe, before gravitational clumping became significant.

Actually, that isn't the case.

Early Universe Cosmology Evidence for Deur's Approach

The most recent paper that I cited above is precisely above the evolution of the early universe, a subject only addressed more tangentially in earlier papers:

Alexandre Deur, "Effect of gravitational field self-interaction on large structure formation" arXiv: 2018:04649 (July 9, 2021) (Accepted for publication in Phys. Lett. B) DOI: 10.1016/j.physletb.2021.136510

As the body text of that article explains:

Fig. 2. Time-evolution of a baryonic overdensity δ. The initial value of δ at the recombination time, t ≈ 3.7 Gyr, is 2 × 10⁻⁵. The band shows the evolution including field SI effects, with the central solid line corresponding to the nominal DM⁻¹(t). The dashed line is the evolution without SI. In neither case, dark matter has been assumed.

The picture for structure growth that emerges from the result showed in Fig. 2 is that at early times, SI [Ed. i.e. gravitational field self interaction] did not influence the Jeans collapse mechanism since the initial overdensities were spherical. Mergings of overdensities would also not be significantly enhanced since density anisotropies would be too small to trigger the onset of SI. At later times, the overdensities lose their spherical symmetry due to mergers and radiative energy dissipation. The SI-enhanced internal binding then accelerates local collapses. As anisotropies become denser, merging rates increase, especially for overdensities that had so far retained their spherical shape. The quantitative analysis shows that the SI-enhanced gravitational interaction is sufficient to form structures reaching the present-day densities, without requiring dark matter. We have considered here the time-evolution of δ and not the related subject of matter's spatial distribution. As shown in Ref. [10], the same formalism also yields a position of the peak of the matter power spectrum of k_eq≃0.014 Mpc⁻¹, in agreement with observations.

The cosmology conclusions in Reference 10 (a prior published paper by Deur, i.e.
A. Deur, Eur. Phys. J. C, 79 (2019), p. 883 arXiv:1709.02481) are as follows:

A. Supernova observations

Explaining supernova observations with GR’s self-interaction is the focus of this article. These observations are that the large-z (0.1 . z . 1.5) supernova apparent luminosities are dimmer, viz their apparent magnitudes are larger, than expected from a homogeneous and isotropic decelerating Universe. This is interpreted as evidence for an accelerating universe, i.e. for Λ > 0. However, we show in this section that lifting the approximations of homogeneity and isotropy can also explain the observations, while keeping Λ = 0. From the luminosity distance DL(z), Eq. (23), the apparent magnitude DL(z)H0 of events can be calculated. Assuming Λ = 0, taking H0 = 68 ± 1 km/s/Mpc, . . . we compute the band shown in Fig. 3. . . . Our calculation agrees well with the γ-ray bursts and supernovae data. There is no adjustment to these data, all the parameters in DM being constrained by observations of large structure evolution. Also shown in the figure are the calculations for the cases of a homogeneous and isotropic Universe with only matter (dotted line), that for an empty Universe (continuous line) and the ΛCDM (dark energy, cold dark matter) model (dashed line). The difference between the observations and the expectation from a homogeneous and isotropic Universe with Λ = 0 is clearer by forming a residual apparent magnitude:

r(z) = 5 log H0 DL(z) 1 + z − 5 log H0 z + z 2/2 1 + z , (27)

with the last term corresponding to the empty Universe case. Positive values of r(z) indicate fainter apparent luminosities than expected in the case of an empty Universe. They constitute the best evidence for Λ > 0. Our calculation of r(z) with Λ = 0 agrees well with the observations.

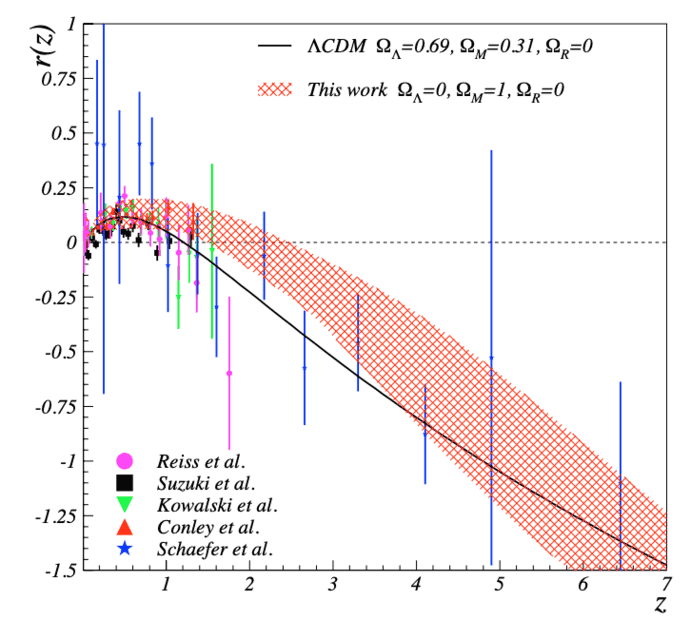
FIG. 4: Residual between observed apparent magnitudes (γ-ray bursts: star symbol. Supernovae: other symbols) and their expectation from an empty universe. The continuous line is for the ΛCDM model. The band is the present work, without any free parameters adjusted to the γ-ray or supernova data.

We now outline how GR’s self-interaction may also explain the observations providing less direct evidence for Λ > 0.

B. Age of the Universe

Without Λ > 0, the calculated age of the Universe would be 11.7 ± 0.2 Gyr for the standard ΩM = 0.32 value and for H0 = 68 ± 1 km/s/Mpc. This conflicts with the measured age of the oldest stars, up to ∼ 13.5 Gyr. The ΛCDM model, with ΩΛ = 0.68 and the same H0 and ΩM values, yields 13.6 ± 0.2 Gyr. GR’s self-interaction also solves this problem, while keeping Λ = 0: Eq. (24) yields a compatible Universe age of 13.2 ± 1.7 Gyr.

C. Large structure formation

In a Universe without gravitational self-interaction or dark matter, large structures do not have time to coalesce. What happens in the self-interaction framework can be sketched as follow: As DM(z) departs from 1, viz as gravity weakens globally, energy conservation demands that the global weakening is balanced locally by an increase of gravity within the structures themselves, thus speeding up their formation compared to a Universe without self-interaction. Since DM(z) evolves following the formation of large structures, gravity strengthens locally with the same timeline. Because strengthening reproduces the dynamics of galaxies and clusters, the local effect of self-interaction is equivalent to the effect of dark matter. Furthermore, the position of the peak of the matter power spectrum is now given by keq = H0 p 2Ω∗ M(0)/aeq, with aeq the scale parameter at zeq. Assuming ΩBaryon = ΩM (no dark matter) and using Ω∗ M = ΩMDM yield Ω∗ M(0) ' 0.3, i.e. k_eq = 0.014, in agreement with observations. This suggests that the present approach is compatible with large structure formation.

D. CMB and BAO

The CMB main acoustic peak position depending on the Universe dynamical evolution, its calculation in the present framework involves Ω∗ M rather than ΩM. Thus we have now θ ' p Ω∗ M/zrec (with zrec ' 1100 at the recombination time), resulting in θ ' 0.8 ◦ , which agrees with observations. Predicting the smaller features of the CMB and the BAO is complex and, like for large structure formation, beyond the scope of this first article.

E. Other consequence

Field trapping naturally explains the cosmic coincidence, i.e. that in the ΛCDM model, dark energy’s repulsion currently nearly compensates matter’s attraction, while repulsion was negligible in the past and attraction is expected be negligible in the future. No natural explanation exists within ΛCDM for this apparently fortuitous coincidence. In the present approach, structure formation depletes attraction and thus, compensating it with a repulsion, viz dark energy, is unnecessary. Thus, there is no coincidence and hence no need for explanation.

It has long been known that modified gravity approaches, generically, tend to solve the "impossible early galaxies" problem of ΛCDM by speeding up structure formation. See, e.g., Llinares et al. 2008 ("we find that the large-scale structure evolution is faster in our revised MOND model leading to an even stronger clustering of galaxies, especially when compared to the standard LCDM paradigm."). See also Sanders 1998, McGaugh 1998, McGaugh 1999, McGaugh 2000, Sanders 2001, Nusser 2002, Stachniewicz & Kutschera 2002, McGaugh 2004, Skordis et al. 2005, Feix 2016, Khoury 2016.

Meanwhile, the ΛCDM model when compared with observational data at the larger cosmology scale also fails the test of the new EDGES 21cm wavelength radiation data that demonstrates the temperature of the universe at 180 million to 280 million years after the Big Bang. This is inconsistent with the ΛCDM model because the universe was much colder than predicted and is instead consistent, generically, with a no dark matter hypothesis.

Also, finally, last year, a relativistic modified gravity theory that reduces to MOND in the limit has reproduced the crown jewel of LambdaCDM, the CMB patterns that are observed. See Constantinos Skordis, Tom Złosnik, "A new relativistic theory for Modified Newtonian Dynamics" arXiv (June 30, 2020). And, given that Deur's model is very close to MOND at the galactic rotation curve level, the likelihood that Deur's approach can achieve the same result is much more plausible than it was two years ago. In another proof of the concept that modified gravity theories can get the CMB right, Moffat's MOG theory did so in 2014.

Other Non-Galaxy Rotation Curve Evidence

Furthermore, keep in mind that unlike many modified gravity theories, this isn't just galaxy rotation curves in addition to this recent paper on the early evolution of the universe discussed above.

It is also planar alignments of satellite galaxies. It is cluster dynamics and the Bullet Cluster. It is all dark energy phenomena (in a manner equivalent to dark energy that is not a pure cosmological constant as the data increasingly slightly favor).

It is providing a theoretical grounding from first principles for phenomena that other gravitationally based approaches to dark matter and dark energy phenomena have only described with phenomenological fits to observations.

Conclusion

One of the things that makes this approach so attractive is that it has a domain of applicability that is broader than almost any other gravity based approach out there right now, with the possible exception of Moffat's MOG theory (which manifestly deviated from GR and designed simply to fit observations without a clear theoretical foundation). MOND doesn't address dark energy or cluster scale phenomena correctly. Meanwhile, many other modified gravity theories proposed by GR researchers provide alternatives to the cosmological constant/dark energy, but don't solve dark matter phenomena.

Also, while there are areas of this approach that simply haven't been developed yet by the sole primary researcher working on this in addition to this day job in QCD physics (e.g. CMB, derivation of MOND constant from Newton's constant, wide binaries, external field effects), there are so far, no instances of clear contradictions with observation, or theoretical inconsistencies that have been identified.

 

[bhobba]

Getting back to the title of the thread. We really only have an effective field theory for gravitons. I think it is too early in our understanding of Quantum Gravity to make any definitive statement. It has been discussed before, discontinued in May, but for some reason revived on August 11.

The mentors will keep an eye on it to see if it adds value to the previous discussion.

Thanks
Bill

 

[ohwilleke]

It has been discussed here before:
https://www.physicsforums.com/threads/do-gravitons-interact-with-gravitons.1002590/

Did you mean to link to this thread?

 

[bhobba]

Did you mean to link to this thread?

Sorry didn't notice it was the same thread. Changed the working to the mentors will keep an eye on if its revival is of any value.

Thanks
Bill

 

[timmdeeg]

After rereading Deur's recent article I came across this text passage where I seem to have a misunderstanding:

Likewise2 in gravitational systems, the increased binding due to GR's SI weakens gravity's action at large scale. If GR's SI is ignored, this weakening can then be misinterpreted as a large-scale repulsion, viz dark energy. The effect is time-dependent: as massive structures form, some gravitational fields become trapped in them, weakening their manifestation at larger scale. This implies a direct connection between dark energy and dark matter, particularly between dark energy and the onset of structure formation.

I "understand" that the " increased binding due to GR's SI" could account for dark matter. But how can the weakening of gravity's action (due to SI) account for the observed accelerated expansion of the universe?

If gravity is "just" weakened between the Galaxy clusters it's still attractive so how can this imitate (or replace?) the action of repelling gravity according to the Lambda-CDM model?

What am I missing?

 

[PeterDonis]

The most recent paper that I cited above is precisely above the evolution of the early universe

I'll take a look, this looks more recent than the Deur papers I am familiar with.

 

[ohwilleke]

After rereading Deur's recent article I came across this text passage where I seem to have a misunderstanding:I "understand" that the " increased binding due to GR's SI" could account for dark matter. But how can the weakening of gravity's action (due to SI) account for the observed accelerated expansion of the universe?

If gravity is "just" weakened between the Galaxy clusters it's still attractive so how can this imitate (or replace?) the action of repelling gravity according to the Lambda-CDM model?

What am I missing?

To slightly oversimplify, DM phenomena are attributed to gravitons staying in the system more often than they would in a spherically symmetric system. Since those gravitons never level the system, there are fewer gravitons leaving the system than would leave a spherically symmetric system. So, the bond between the two systems is weaker than one would expect. Not being held together a tightly due to weaker than expected gravitational fields between systems looks the same as being pulled apart by additional diffuse dark energy.

 

[PeterDonis]

To slightly oversimplify, DM phenomena are attributed to gravitons staying in the system more often than they would in a spherically symmetric system. Since those gravitons never level the system, there are fewer gravitons leaving the system than would leave a spherically symmetric system. So, the bond between the two systems is weaker than one would expect. Not being held together a tightly due to weaker than expected gravitational fields between systems looks the same as being pulled apart by additional diffuse dark energy.

This explanation has at least two issues.

First, since Deur has also claimed that his proposed effect (at least, the one that emulates dark matter--see below) can be derived in classical GR, any talk about "gravitons" is both superfluous (we don't need any quantum gravity effects) and potentially misleading (since we have no actual evidence for any quantum gravity effects). In classical GR terms, Deur's proposed effect is due to nonlinearities in the Einstein Field Equation causing additional effects in a lens-shaped or disk-shaped system that they do not cause in a spherically symmetric system (because the additional symmetry basically cancels them out). I think that is a much better heuristic picture than any picture involving "gravitons".

Second, dark energy is not the same as dark matter. The "nonlinear effects" part, as I described it above, is a proposed alternate explanation for effects that are attributed in our current standard cosmology to dark matter. But the "fewer gravitons leaving the system" part is a proposed alternate explanation for effects that are attributed in our current standard cosmology to dark energy, not dark matter. The latter alternate explanation, AFAIK, is on much shakier ground since it does not appear in the classical version of Deur's proposal (i.e., it is not an effect that appears in classical GR; it is not just due to nonlinearities in the EFE, but something else). I think it would be much better not to conflate the two.

 

[ohwilleke]

This explanation has at least two issues.

First, since Deur has also claimed that his proposed effect (at least, the one that emulates dark matter--see below) can be derived in classical GR, any talk about "gravitons" is both superfluous (we don't need any quantum gravity effects) and potentially misleading (since we have no actual evidence for any quantum gravity effects). In classical GR terms, Deur's proposed effect is due to nonlinearities in the Einstein Field Equation causing additional effects in a lens-shaped or disk-shaped system that they do not cause in a spherically symmetric system (because the additional symmetry basically cancels them out). I think that is a much better heuristic picture than any picture involving "gravitons".

I don't disagree that the effect can be derived in classical GR which lacks gravitons. But, as a quick and dirty way to get across the concept, I think it is much more natural to understand in a graviton context, which is why I used this heuristic with the caveat that I am oversimplifying.

Ultimately, the physics of massless spin-2 gravitons are identical to GR except for quantum effects not implicated in this context, and the static equilibrium approximation used by Deur is, in this context, not sacrificing any important effects relevant to dark matter or dark energy phenomena.

Second, dark energy is not the same as dark matter. The "nonlinear effects" part, as I described it above, is a proposed alternate explanation for effects that are attributed in our current standard cosmology to dark matter. But the "fewer gravitons leaving the system" part is a proposed alternate explanation for effects that are attributed in our current standard cosmology to dark energy, not dark matter. The latter alternate explanation, AFAIK, is on much shakier ground since it does not appear in the classical version of Deur's proposal (i.e., it is not an effect that appears in classical GR; it is not just due to nonlinearities in the EFE, but something else). I think it would be much better not to conflate the two.

The non-linearities in classical GR have the same effect, although much less transparently, which is why I didn't use that heuristic example.

From the perspective of classical GR, the strengthening of the fields within the system due to its asymmetries and the non-linearities of GR that gives rise to dark matter phenomena simultaneously weakens the gravitational fields by a like amount outside that system.

The July 9, 2021 paper explains:

Besides their fundamentally different interpretation of the nature of gravitation, GR and Newton's gravity also crucially differ in that GR is non-linear. This can be traced to field SI once space-time curvature is interpreted in terms of fields. GR can be formalized by the Einstein-Hilbert Lagrangian density,(1)LGR=(det⁡gμν)12gμνRμν/(16πG),with gμν the metric, Rμν the Ricci tensor and G the gravitational constant. The https://www.sciencedirect.com/topics/physics-and-astronomy/gravitational-fields φμν originating from a unit mass source is the variation of gμν with respect to a constant metric ημν: φμν=(gμν−ημν)/M, where M is the system mass. Expanding LGR in term of φμν yields, in the pure field case [12]:(2)LGR=[∂φ∂φ]+16πMG[φ∂φ∂φ]+16πMG[φ2∂φ∂φ]+⋯,where [φn∂φ∂φ] represents a sum of Lorentz-invariant terms of the form φn∂φ∂φ. Newton's gravity is given by LGR truncated to n=0, with [∂φ∂φ]=∂μφ00∂μφ00, ημν the flat metric and ∂0φ00=0. The n>0 terms induce field SI.

Another fundamental force displaying SI is the Strong Interaction. It is formalized by quantum chromodynamics (QCD) whose pure field Lagrangian is:(3)LQCD=[∂ϕ∂ϕ]+παs[ϕ2∂ϕ]+παs[ϕ4].Here, ϕμ is the gluonic field and αs the QCD coupling [13]. Again, a bracket [] indicates a sum of Lorentz-invariant terms, and, in the QCD case, contractions of the color indices. The similarity between LGR and LQCD makes the latter useful as a guide for GR in its strong regime, since QCD in that regime is well-studied. Like GR, the terms beyond [∂ϕ∂ϕ] induce the field SI. They are interpreted in QCD (GR) as arising from the color charges (energy-momentum) carried by gluonic (gravitational) fields, which permit field self-coupling. For QCD the coupling –driven by αs– is large, making the consequences of field SI prominent. In GR, large GM/L values (L is a characteristic length of the system) enable SI. QCD's SI strongly increases the interaction between color charges and causes quark confinement. Likewise, GR's SI increases the gravitational system's binding compared to Newton's theory. If the latter is used to analyse galaxy or cluster dynamics, as is commonly done, ignoring the SI-induced intensification of the force then creates a missing (dark) mass problem. The results of Refs. [6], [7], [8] indicate that SI can sufficiently strengthen the gravitational binding such that no dark matter is required to explain galactic rotation curves or the internal dynamics of galaxy clusters. In QCD, the SI strengthens so much the binding of color sources that they remain confined, i.e. the Strong Interaction is essentially1 suppressed outside of the system, e.g. outside a nucleon. This can be globally understood from energy conservation: the confined field increases the system's binding energy, but the field concentration causes its depletion outside of the system. Likewise2 in gravitational systems, the increased binding due to GR's SI weakens gravity's action at large scale. If GR's SI is ignored, this weakening can then be misinterpreted as a large-scale repulsion, viz dark energy. The effect is time-dependent: as massive structures form, some gravitational fields become trapped in them, weakening their manifestation at larger scale. This implies a direct connection between dark energy and dark matter, particularly between dark energy and the onset of structure formation.

 

[PeterDonis]

From the perspective of classical GR, the strengthening of the fields within the system due to its asymmetries and the non-linearities of GR that gives rise to dark matter phenomena simultaneously weakens the gravitational fields by a like amount outside that system.

This is not correct, at least not if "weakens" is taken to mean "causes an effect that looks like accelerating expansion of the universe". In classical GR, what you are calling "strengthening of fields within the system" makes the system more tightly bound and thus decreases its externally measured mass. However, this decrease in externally measured mass, in classical GR, only has the effect of decreasing the deceleration of expansion due to that massive body. It does not cause any effect that looks like accelerating expansion. That requires a different form for the stress-energy tensor, a form which cannot be produced in classical GR simply by making a system more tightly bound.

 

[ohwilleke]

This is not correct, at least not if "weakens" is taken to mean "causes an effect that looks like accelerating expansion of the universe". In classical GR, what you are calling "strengthening of fields within the system" makes the system more tightly bound and thus decreases its externally measured mass. However, this decrease in externally measured mass, in classical GR, only has the effect of decreasing the deceleration of expansion due to that massive body. It does not cause any effect that looks like accelerating expansion. That requires a different form for the stress-energy tensor, a form which cannot be produced in classical GR simply by making a system more tightly bound.

To be clear, you don't disagree with the notion of a "decrease in externally measured mass, in classical GR," which is the effect that he is referencing.

Keep in mind that this decrease is present and growing (on average) with respect to every single galaxy and galaxy cluster and other gravitationally bound system. Certainly, a weaker gravitational bond between galaxies and galaxy clusters across the board looks the same as Newtonian gravity plus a repulsive force.

It is not at all obvious why "the deceleration of expansion due to that massive body. It does not cause any effect that looks like accelerating expansion". If clumps of matter have an initial expansion rate at one level of gravitational bonding which is holding back the momentum driving the initial expansion, and the gravitational bond between those clumps of matter weakens over time, why shouldn't it appear to accelerate relative to the rate seen before, with the same momentum but less of a gravitational force between clumps of matter holding it back.

 

[PeterDonis]

this decrease is present

Only in the sense that the actual mass is less than the mass currently included in our models.

and growing

Not as I understand it. A galaxy with a given number of stars will have a given "decrease" (actual mass compared to mass in our current models) that does not change.

a weaker gravitational bond between galaxies and galaxy clusters

Is not the actual classical GR effect. The actual classical GR effect is a slightly smaller mass for each galaxy and galaxy cluster than the one that is currently in our models. That is not the same as a "weaker gravitational bond". The "strength of gravity" is not changed. See below.

looks the same as Newtonian gravity plus a repulsive force.

No, it doesn't. It looks like a slightly smaller "matter" contribution to the overall evolution of the FRW spacetime scale factor than the one that is in our current models. There is no "repulsive force". The effect of the matter contribution on the evolution of the scale factor (namely, deceleration) is not changed.

It is not at all obvious...

Maybe not to you, but that does not mean you should resort to hand-waving to try to justify your alternative claim. You should stop and think very carefully about what the "decrease" you refer to actually means. See my comments above.

 

[ohwilleke]

Not as I understand it. A galaxy with a given number of stars will have a given "decrease" (actual mass compared to mass in our current models) that does not change.

Galaxies merge and collect into galaxy clusters over time. The number of stars in the system grows. As the systems evolve to have stronger dark matter phenomena over time, the magnitude of the dark energy phenomena increases as well.

No, it doesn't. It looks like a slightly smaller "matter" contribution to the overall evolution of the FRW spacetime scale factor than the one that is in our current models. There is no "repulsive force".

I'm not saying that there is a repulsive force, I'm saying that if you have one force between two objects that weakens, that is indistinguishable observationally from a stronger force that is expected matched by a repulsive force.

Think of it this way. Our current observations are incorporated into a model to estimate the magnitude of lambda, the cosmological constant. If the apparent masses of galaxies at the same distance from each other is smaller than previously modeled, and if that apparent mass decreases over time due to galaxy mergers, galaxy cluster formation, etc., the estimated value of lambda should be smaller than it is currently estimated as being today. Also, this particular physical constant is one of the less precisely known in core theory. Maybe it goes to zero, much it is just materially smaller and we still need "dark energy" albeit, much less of it. Somebody has to quantify the exact magnitude of that effect which Deur tries to do in his latest paper. But, it is hard to see how it could not be a significant adjustment. The amount of energy required to make the expansion accelerate at an observed rate has to be smaller if the amount of apparent mass that needs to be moved is smaller.

 

[PeterDonis]

Galaxies merge and collect into galaxy clusters over time. The number of stars in the system grows. As the systems evolve to have stronger dark matter phenomena over time, the magnitude of the dark energy phenomena increases as well.

Ah, I see.

I'm not saying that there is a repulsive force, I'm saying that if you have one force between two objects that weakens, that is indistinguishable observationally from a stronger force that is expected matched by a repulsive force.

This is not correct, because here "repulsive force" would have to mean "something that causes the appearance of accelerated expansion", and that's not what a change to the matter term in the evolution equation for the scale factor does. All it does is reduce the deceleration. It does not change deceleration to acceleration. Those are qualitatively different appearances and one cannot reproduce the other.

 

[PeterDonis]

The amount of energy required to make the expansion accelerate at an observed rate has to be smaller if the amount of apparent mass that needs to be moved is smaller.

This is not correct. Accelerated expansion is not a "force" that has to be bigger to move more mass. It is a geometric property of spacetime that affects geodesic deviation, independently of the masses of objects that might or might not be following such geodesics.

 

[timmdeeg]

All it does is reduce the deceleration. It does not change deceleration to acceleration. Those are qualitatively different appearances and one cannot reproduce the other.

Thanks, much better expressed than what I tried to say in #35.

I really wonder if/why Deur has overlooked this issue.

 

[PeterDonis]

I really wonder if/why Deur has overlooked this issue.

I don't know that Deur has. I only know that @ohwilleke is. I don't know that Deur makes all of the same claims in his papers that @ohwilleke is making in this thread.

 

[timmdeeg]

I don't know that Deur has. I only know that @ohwilleke is. I don't know that Deur makes all of the same claims in his papers that @ohwilleke is making in this thread.

It seems that Deur makes this claim.

https://www.sciencedirect.com/science/article/pii/S0370269321004500?via=ihub

Ref. [10] points out that the SI-enhanced binding inside massive systems is balanced by reduced gravitational field outside these systems, and shows how this reduction can explain without dark energy the large-z supernova observations [18].

As I understand it these observations are uncontroversially associated with the accelerated expansion of the universe. Deur doesn't mention this term though.

 

[PeterDonis]

It seems that Deur makes this claim.

Yes, I see. Ref. 10 is this paper:

https://arxiv.org/abs/1709.02481

I'll take a look at it.

 

[PeterDonis]

Deur doesn't mention this term though.

He does in the first sentence of the paper I linked to in post #49.

 

[timmdeeg]

So he says implicitly that the "reduced gravitational field outside these systems" can explain the accelerated expansion of the universe.

 

[PeterDonis]

So he says implicitly that the "reduced gravitational field outside these systems" can explain the accelerated expansion of the universe.

That's how it looks to me, yes; but I'm not entirely sure whether, in his model, the term "accelerated expansion" is actually a correct description. He might be implicitly saying that what we currently think of as "accelerated expansion" is actually not accelerated, but it appears to us to be because we are modeling the evolution of the scale factor incorrectly; in Deur's model, the evolution of the scale factor might be changed so the expansion actually never is accelerated, we are just interpreting our observations incorrectly.

 

[ohwilleke]

Ah, I see.This is not correct, because here "repulsive force" would have to mean "something that causes the appearance of accelerated expansion", and that's not what a change to the matter term in the evolution equation for the scale factor does. All it does is reduce the deceleration. It does not change deceleration to acceleration. Those are qualitatively different appearances and one cannot reproduce the other.

"Repulsive force" would mean "something that causes an increase in the magnitude to the relative velocity of two masses that tends to move them farther apart from each other. Whether this means "accelerated expansion" or not would depend on exactly how one defined "expansion". Geometric terminology and force terminology are not inherently inconsistent.

 

[PeterDonis]

"Repulsive force" would mean "something that causes an increase in the magnitude to the relative velocity of two masses that tends to move them farther apart from each other.

That's the same thing as "accelerating expansion"; "accelerating" means "increasing magnitude of velocity".

As I noted in post #52, however, it's not clear to me whether Deur is actually claiming that. It seems to me that he might be saying that our universe's expansion actually is not accelerated--that the relative velocity between comoving observers is not actually increasing. He might be saying that it only appears to be increasing because our current standard model, the Lambda CDM model, is using an incorrect method of deriving the scale factor as a function of time, and when Deur's method is used instead, we find a different function of time for the scale factor, one which is always decelerating.

 

[timmdeeg]

It seems to me that he might be saying that our universe's expansion actually is not accelerated--that the relative velocity between comoving observers is not actually increasing.

I think this view fits to Deur's recent paper:

https://arxiv.org/pdf/1709.02481.pdf

This increased binding must, by energy conservation, weaken the action of gravity at larger scale. This can then be mistaken for a repulsion, i.e. dark energy. Specifically, the Friedmann equation for an isotropic and homogeneous Universe is (for a matter-dominated flat Universe) H2 = 8πGρ/3, with H the Hubble parameter and ρ the density. As massive structures coalesce, gravity is effectively suppressed at scales larger that these structures. This weakening with time results in a larger than expected value of H at early times, as seen by the observations suggesting the existence of dark energy.

 

[PeterDonis]

I think this view fits to Deur's recent paper

Yes, that's one of the statements that makes me think that. I'm still working through the actual math.

 

[timmdeeg]

I'm still working through the actual math.

Great.

Perhaps it's possible to see if in principle Deur's model predicts observations which could verify/falsify his claim.

 

[ohwilleke]

Great.

Perhaps it's possible to see if in principle Deur's model predicts observations which could verify/falsify his claim.

There are many such observations at the galaxy scale (e.g. the relationship between the extent that an elliptical galaxy is spherical and its apparent dark matter fraction, and a relationship in spiral galaxies related to disk thickness), but the dark energy/cosmology scale work is less worked out. The main prediction seems to be structure formation at an earlier time than LambdaCDM which does indeed have some support observationally.

 

[timmdeeg]

The main prediction seems to be structure formation at an earlier time than LambdaCDM which does indeed have some support observationally.

Yes, but besides that I had the Ia Supernovae data and the CMB Power Spectrum in my mind. I wonder if the depletion function which is based on anisotropy factors shouldn't in principle produce the SN data. As Deur claims that these data are "mistaken for repulsion" then I would expect that e.g. the depletion function should yield an alternative (quantitative) explanation.

 

[ohwilleke]

Yes, but besides that I had the Ia Supernovae data and the CMB Power Spectrum in my mind. I wonder if the depletion function which is based on anisotropy factors shouldn't in principle produce the SN data. As Deur claims that these data are "mistaken for repulsion" then I would expect that e.g. the depletion function should yield an alternative (quantitative) explanation.

I'm pretty much 100% certain that the answer is that Deur hasn't had the time and resources to explore a lot of those questions yet. I've corresponded with him in the past and he's basically said as much. The gravity work, while Nobel Prize material and Stephen Hawking class fame generating if it works out, doesn't have grant funding and is basically side hustle made possible by the time that his day job allows for discretionary research. So, he has to spend most of his time working on far less consequential, but better funded, activities. If I won the lottery, the first thing I'd do would be to set up grants or an endowment to support this line of research.