Do Streamlines Change Shape Depending on Frame of Reference in Fluid Dynamics?

[member 428835]

Hi PF!

I read that streamlines around a body change according to one's frame of reference. If we consider a sphere that is moving in a flow (low Re) would the streamlines change shape as we change our reference frame from being on the ball verses sitting aside and watching the ball move past us?

I think the two would look basically the same: the streamlines from the ball's frame of reference would look steady and wrap around the ball in an orderly fashion, where the streamlines from a sitting observer's perspective would appear to "move backwards" so as to constantly wrap around the ball.

Any ideas?

Edit: I just found these two images from a paper here: http://webspace.clarkson.edu/projects/crcd/me537/downloads/02_Pastsphere.pdf
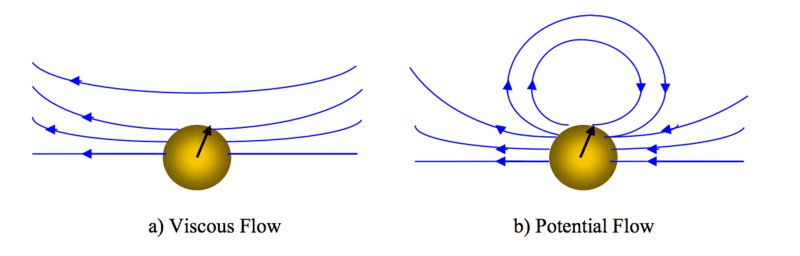
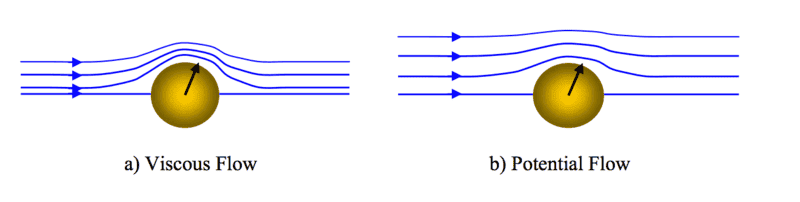
The top images are in a moving frame of reference and the bottom two are in a stationary frame (I assume stationary implies as seen from the sphere). Can someone explain these? Perhaps @boneh3ad or @Chestermiller

 

[boneh3ad]

The top pictures are the streamlines as viewed by a stationary observer. The bottom pictures are the streamlines as viewed by an observer moving with the ball. The top is basically the equivalent of subtracting the free-stream velocity from the bottom images. Basically, if you sit still and watch a ball pass, it will push a fluid particle away from its front, and then the particle will wrap back around the ball (or try to) due to the pressure gradient and end up fairly close to where it started (exactly where it started for potential flow).

 

[member 428835]

Basically, if you sit still and watch a ball pass, it will push a fluid particle away from its front, and then the particle will wrap back around the ball (or try to) due to the pressure gradient and end up fairly close to where it started (exactly where it started for potential flow).

So for the upper figures are you suggesting that the curved streamlines are actually parts of a circle that will reconnect? This is evident for the upper right, but the upper left doesn't seem like it would ever attach to itself.

 

[boneh3ad]

So for the upper figures are you suggesting that the curved streamlines are actually parts of a circle that will reconnect? This is evident for the upper right, but the upper left doesn't seem like it would ever attach to itself.

Well those pictures are clearly not computed streamlines. They are hand-drawn for illustrative purposes. In a viscous flow, the ball would drag some of the fluid with it, so a fluid particle would likely still loop around, but it would end at a different location upstream of where it started (upstream as in further along the ball's movement path, which is upstream in the case of the stationary ball frame).

 

[member 428835]

Thanks, that makes a lot of sense!

 

[dimasmr21]

Hi, i want to know if there is any reference regarding the derivation of this velocity potential.
By which i mean the problem of "flow around a moving cylinder". I want to derive the velocity potential of the fluid around a moving cylinder.

Thank you !

 

[BvU]

Hi, i want to know if there is any reference regarding the derivation of this velocity potential.
By which i mean the problem of "flow around a moving cylinder". I want to derive the velocity potential of the fluid around a moving cylinder.

Thank you !

Post a new thread.

 

[dimasmr21]

Post a new thread.

sorry, i will start a new thread.