rakeru
- 75
- 0
Homework Statement
Use a graphing calculator to find \delta
when
0<|x - \pi/2|<\delta and |sin(x) - 1|<0.2
Homework Equations
I don't think there are any other than the format of the previous information:
0<|x-a|<\delta and |f(x)-L|<\epsilon
The Attempt at a Solution
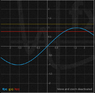
Okay, so I used the graphing calculator to graph sinx, y=1.2 and y=0.8
The thing is, L + ε turns out to be greater than 1, so I have something like this (i attached a picture).
For \delta I got 0.61. I'm not sure if it's possible, because the line y=1.2 doesn't touch the graph of sinx. Is it possible?
Thank you!