Does Tension Increase with Higher Angles in a String?

[chopnhack]

This is a general question about tension in a string. If we have a string that makes an angle theta of 10 degrees with the vertical, what would the tension in the string be.

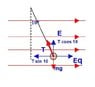
If we assume a mass of 0.025kg at the end of 0.8m long string, I calculate that the force acting opposite mass x gravity would be Tcos10degrees. If we rewrite this to solve for T = 0.245N/cos 10

My question comes from an observation, as we take values of higher angles, nearly horizontal for instance, cos 89 (perpendicular to the vertical axis) = 0.01745. If we divide 0.245N by this value we get a number much larger than the original when tension should be nearly zero.

The picture is from the solution to the example where the thought arose from.

 

[scottdave]

Most of the tension in the string is in the horizontal direction. In order to provide the proper amount of force in the vertical direction, the tension must be much higher at these near horizontal angles.

 

[chopnhack]

Most of the tension in the string is in the horizontal direction. In order to provide the proper amount of force in the vertical direction, the tension must be much higher at these near horizontal angles.

What your saying is that its proportional - for the angle to be at that level, the tension would need to be commensurate and hence the force would need to be much higher. It makes more sense now. Thank you!