Why used $\cos\theta$ for $\text{y}$ axis or, gravitational force?

[Istiak]

Homework Statement

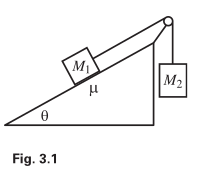
Mass M1 is held on a plane with inclination
angle θ, and mass M2 hangs over the side. The two masses are connected by a
massless string which runs over a massless pulley (see Fig. 3.1). The coefficient of
kinetic friction between M1 and the plane is µ. M1 is released from rest. Assuming that
M2 is sufficiently large so that M1 gets pulled up the plane, what is the acceleration
of the masses? What is the tension in the string?

Relevant Equations

F=ma

><br/>
>Mass M1 is held on a plane with inclination
angle θ, and mass M2 hangs over the side. The two masses are connected by a
massless string which runs over a massless pulley (see Fig. 3.1). The coefficient of
kinetic friction between M1 and the plane is µ. M1 is released from rest. Assuming that
M2 is sufficiently large so that M1 gets pulled up the plane, what is the acceleration
of the masses? What is the tension in the string?

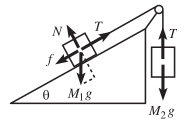
Then, they were writing force of that figure.

$$T-f-M_1g\sin \theta = M_1a$$
$$N-M_1g\cos \theta=0$$
$$M_2g-T=M_2a$$

In the second equation they wrote that $$M_1g\cos \theta$$

Usually, $\cos$ is used when we think of $\text{x}$ axis. Since, $$\cos \theta=\frac{\color{blue}\text{base}}{\text{hypotenuse}}$$
But, gravitational force is forever through $\text{y}$ axis. Although, why they used $\cos\theta$ for gravitational force.

 

[PeroK]

Force is a vector and can be decomposed into components tangential to and normal to a slope. That's why an object tends to move down a slope with less than the free fall acceleration.

As in your other post, it looks like it's the concept of vector components you are missing.

 

[haruspex]

Usually, $\cos$ is used when we think of ${x}$ axis.

That is the case when starting with something (a force, a displacement..) at angle theta to the horizontal and finding the horizontal component: $x=r\cos(\theta)$.
In this case, we are starting something vertical (weight) and finding its component normal to the slope. That is the same as the angle between the plane and the horizontal.