Does the postulate of equal a priori probability apply only to equilibrium?

[Jeremy1986]

In deducing the zeroth law of thermodynamics in micro-canonical ensemble, there is a frequently-mentioned example. Suppose we put two isolated system, system 1 and 2, in contact and allowing them to exchange heat.

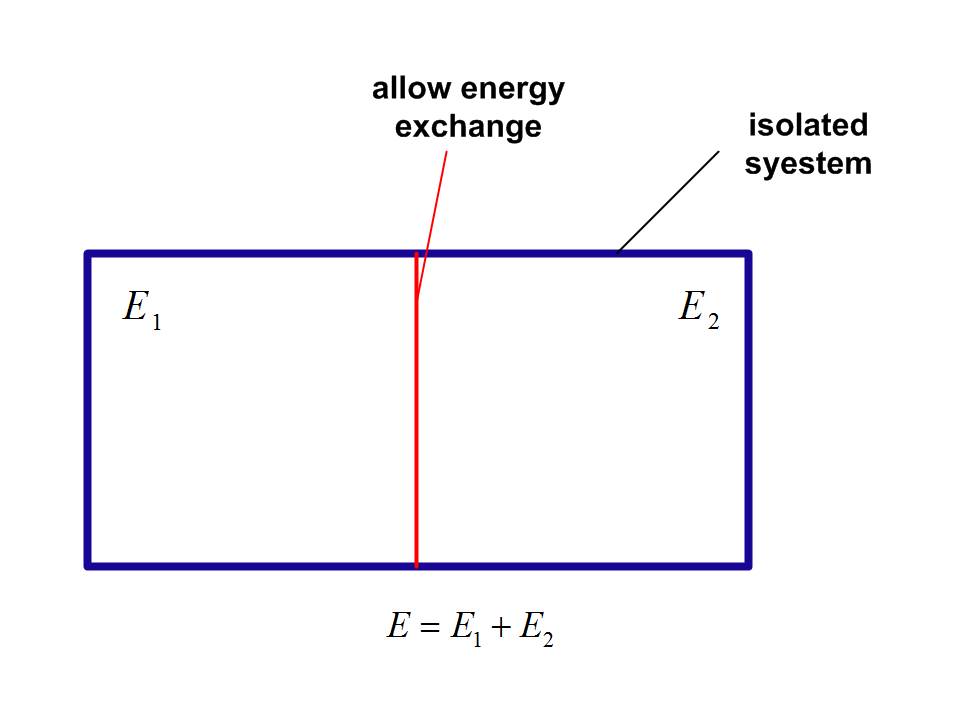The total energy of the combined system is

$$E = {E_1} + {E_2}$$

The total allowed phase space is

$$\Omega (E) = \int d {E_1}{\Omega _1}({E_1}){\Omega _2}(E - {E_1}) = \int d {E_1}\exp [\frac{{{S_1}({E_1}) + {S_2}(E - {E_1})}}{{{k_B}}}]$$

By taking the maximum of the integrand,

$$\frac{{\partial {S_1}({E_1})}}{{\partial E}} + \frac{{\partial {S_2}(E - {E_1})}}{{\partial E}} = 0$$

we get the equilibrium state $(E_1^{eq},E - E_1^{eq})$, which is the macrostate with exponetially larger number of microstates, and also get the equilibrium condition

$$\frac{{\partial {S_1}({E_1})}}{{\partial {E_1}}} = \frac{{\partial {S_2}(E - {E_1})}}{{\partial {E_2}}}$$---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

The equal a priori probability postulate, as descripted by David Tong p4 , is

For an isolated system in equilibrium, all accessible microstates are equally likely.

So my question is, does that mean the microsates corresponds to the equilibrium macrosate $(E_1^{eq},E - E_1^{eq})$ possses equal probability or all the microstates with constant $E$ (the blue line in next figure) possesses equal probability?

For me, it looks like every reference I found indicates the second statement. But for a microsate corresponds to $(E_1^{0},E - E_1^{0})$ which is not at equilibrium, does it have the same probability as a microstate of $(E_1^{eq},E - E_1^{eq})$?

 

[mfb]

If you consider the microstates of the combined system then everything with the same energy should have the same volume. If you consider the microstates of one system this is no longer true. As an example, a microstate with a very high energy in one volume needs a microstate with low energy in the other volume - but typically there won't be many of them.

 

[Michael Price]

Yes. Equi-probable states maximise the Gibbs formula for entropy, the most general and universal formula for entropy. This ensures equilibrium.
Gibbs: S= - k Σp ln(p)
Hence
Boltzmann: S= k ln(W). At equilibrium.
W=number of microstates.

Works for everything: gases, liquids, solids, black holes etc etc

 

[Lord Jestocost]

Personally, I prefer the following statement:

“If an isolated system is found with equal probability in each accessible microstate, then it is in equilibrium. Starting with this distribution, it stays that way. This is what we mean by thermal equilibrium.” (from the Lecture Note about the “Microcanonical Ensemble” by John McGreevy, https://mcgreevy.physics.ucsd.edu/s12/index.html)

The statement is thus about a distribution. It is not about the microstates which realize a certain energy combination $(E_1^{eq},E - E_1^{eq})$ when one considers, for example, a combined isolated system consisting of two sub-systems which can exchange energy with each other. $E_1^{eq}$ means nothing else than that it is overwhelmingly likely to find system 1 with energy $E_1^{eq}$ in course of time in thermal equilibrium.

 

[vanhees71]

Indeed, the maximum-entropy solution is the equilibrium. This becomes much more transparent later in the stat-mech lecture when you study non-equilibrium situations. The Boltzmann equation together with unitarity of the S-matrix gets you the principle of detailed balance (the weak form is enough!), and this leads to the H theorem (to be pronounced as "Eta theorem"), i.e., that the entropy cannot decrease and thus that equilibrium is reached at maximum entropy. The best discussion about this point I know is in Landau&Lifshitz Vol. 10.

 

[Jeremy1986]

If you consider the microstates of the combined system then everything with the same energy should have the same volume. If you consider the microstates of one system this is no longer true. As an example, a microstate with a very high energy in one volume needs a microstate with low energy in the other volume - but typically there won't be many of them.

Thank mfb for your kind reply! I think maybe my misunderstanding was that equilibrium does not correspond to microstate.

 

[Jeremy1986]

Yes. Equi-probable states maximise the Gibbs formula for entropy, the most general and universal formula for entropy. This ensures equilibrium.
Gibbs: S= - k Σp ln(p)
Hence
Boltzmann: S= k ln(W). At equilibrium.
W=number of microstates.

Works for everything: gases, liquids, solids, black holes etc etc

Thank Michael for your kind reply! I think maybe my misunderstanding was that equilibrium does not correspond to microstate.

 

[Jeremy1986]

Personally, I prefer the following statement:

“If an isolated system is found with equal probability in each accessible microstate, then it is in equilibrium. Starting with this distribution, it stays that way. This is what we mean by thermal equilibrium.” (from the Lecture Note about the “Microcanonical Ensemble” by John McGreevy, https://mcgreevy.physics.ucsd.edu/s12/index.html)

The statement is thus about a distribution. It is not about the microstates which realize a certain energy combination $(E_1^{eq},E - E_1^{eq})$ when one considers, for example, a combined isolated system consisting of two sub-systems which can exchange energy with each other. $E_1^{eq}$ means nothing else than that it is overwhelmingly likely to find system 1 with energy $E_1^{eq}$ in course of time in thermal equilibrium.

Thank you very much for your excellent reply! Also many thanks to the provided useful references. I think I start to know the answer to my question after reading your reply. I think the key point is that equilibrium is a macroscopic property which we can't say a microscopic state is at equilirium or not. In an equilibrium ensemble with many microstates, there could be some "non-equilibrium microstates" whose energy does not corresponds to equilibrium states (likes the microscopic states with energy $(E_1^{0},E - E_1^{0})$ or the microstate that all gas atoms stay in the left box), and this is the source of fluctuation. But since we have the equal priority probability postulate, what the system arises is the most probable microstates which has the equilibrium condition
$$\frac{{\partial {S_1}({E_1})}}{{\partial {E_1}}} = \frac{{\partial {S_2}(E - {E_1})}}{{\partial {E_2}}}$$

 

[Jeremy1986]

Indeed, the maximum-entropy solution is the equilibrium. This becomes much more transparent later in the stat-mech lecture when you study non-equilibrium situations. The Boltzmann equation together with unitarity of the S-matrix gets you the principle of detailed balance (the weak form is enough!), and this leads to the H theorem (to be pronounced as "Eta theorem"), i.e., that the entropy cannot decrease and thus that equilibrium is reached at maximum entropy. The best discussion about this point I know is in Landau&Lifshitz Vol. 10.

Thank vanhees71 for your kind reply! I think I start to understand the answer to my question as I wrote it in the reply to Lord Jestocost