physicsfan999
- 1
- 0
- Homework Statement
- A bat flying at 4.10 m/s is chasing an insect flying in the same direction. The bat emits a 40.0-kHz chirp and receives back an echo at 40.4 kHz. (Take the speed of sound in air to be 340 m/s.)
- Relevant Equations
- f_o=f_s(v+v_o/v-v_s)
I'm struggling a lot with this problem on the Doppler effect. I understand the first step which is to treat the bat as the source of the emitted sound, giving
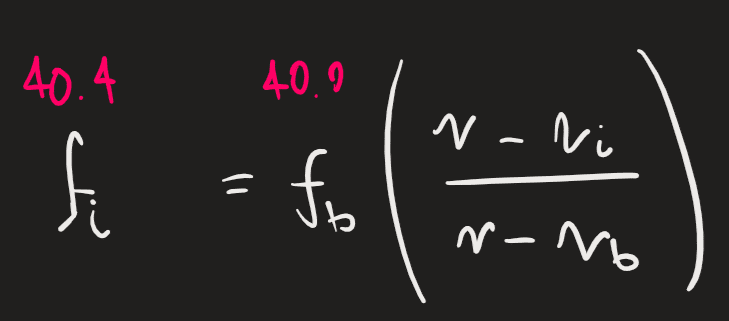
And the second to treat the bat now as the observer, but instead of using f_b on the left the solution involves setting both frequencies to the reflected wave.

I understand there should 2 different variables here for the equation to make sense but I need help understanding why the second step involves setting the two frequencies the same. Thanks in advance!
And the second to treat the bat now as the observer, but instead of using f_b on the left the solution involves setting both frequencies to the reflected wave.
I understand there should 2 different variables here for the equation to make sense but I need help understanding why the second step involves setting the two frequencies the same. Thanks in advance!