Drawing a pre-defined triangle that touches 3 pre-defined lines at all 3 points

[Alaskan Son]

This is my first time posting here so please forgive me any indiscretions...

I'm actually not a student. I'm a general contractor. Part of what I do for a living is draw plans, and that quite often involves geometrical and trigonometrical type challenges. For the most part, I'm usually able to get them figured out, but this one has me stumped, and I didn't know where else to go for help. What I'm trying to do is this:

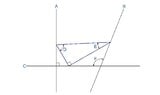
I would like to know the easiest and most intuitive way to figure out how to take a pre-defined triangle and position it so that the 3 points perfectly contact the 3 lines...
View attachment 8170

I'm not super advanced mathematically speaking. I usually just draw circles and lines to figure stuff like this out, but this one has just proven to be more than I can handle. Any help anyone could give me, and in the simplest terms possible, would be absolutely appreciated. Thank you so much for your time.

Michael

 

[I like Serena]

Hi Michael and welcome to MHB! (Wave)

Can we assume that the size of the triangle is fixed?
And that the distance between lines A and B along line C is also fixed?

 

[Alaskan Son]

Hi Michael and welcome to MHB! (Wave)

Can we assume that the size of the triangle is fixed?
And that the distance between lines A and B along line C is also fixed?

That is correct.

 

[I like Serena]

That is correct.

Suppose we label those fixed lengths with $a$, $b$, and $c$ as in the following diagram.
\begin{tikzpicture}[>=stealth]
\draw rectangle (0.3,0.3);
\draw[shift={(1,0)},rotate=atan(1/2)] rectangle (0.3,0.3);
\draw[ultra thick] (-2,0) -- (8,0);
\draw[ultra thick] (0,-3) -- (0,6);
\draw[ultra thick] (5,-3) -- (8,6);
\draw[ultra thick] (0,2) -- node

{a} (1,0) -- node[above left] {b} (7,3) -- cycle;
\draw[gray] (7,0) -- (7,3);
\path[gray] (0,0) -- node[below] {x} (1,0) -- node[below] {c-x} (6,0) -- (7,0) -- node

{y} (7,3);
\path (0,0) -- node[below,yshift=-8] {c} (6,0);
\path (1,0) +({atan(1/2)/2}:0.8) node {$\phi$};
\path (0,2) +({270+atan(1/2)/2}:0.8) node {$\phi$};
\path (6,0) node[above left] {F};
\draw[<->] (6,0) +(-0.8,0) arc (180:atan(3):0.8);
\end{tikzpicture}

And let's define $x$, $y$, and $\phi$ as in the diagram as well.

Now let me run through the steps and I suggest you ask for clarification for steps that you don't understand.

We can set up a system of equations based on trigonometry:
\begin{cases}a\sin\phi = x \\ b\sin\phi = y \\ b\cos\phi = (c-x) + y\cdot\cot(\pi-F)\end{cases}

It follows that:
$$\sin\phi=\frac yb \\ x=a\cdot\frac yb \\ \cos\phi= \sqrt{1-\sin^2\phi}=\sqrt{1-\frac{y^2}{b^2}} \\
\cot(\pi-F)=-\cot F
$$
If we substitute that in the 3rd equation we get:
$$b\sqrt{1-\frac{y^2}{b^2}}=c-a\cdot\frac yb-y\cdot\cot F \quad\Rightarrow\\
b^2-y^2=\left(c-\left(\frac ab+\cot F\right)y\right)^2 = c^2 -2c\left(\frac ab+\cot F\right)y + \left(\frac ab+\cot F\right)^2y^2 \quad\Rightarrow\\
\left(\left(\frac ab+\cot F\right)^2+1\right)y^2 -2c\left(\frac ab+\cot F\right)y + (c^2 - b^2)=0\\
$$
This is a quadratic equation in $y$ that we can solve with the quadratic formula.
After that we can also find $x$ and $\phi$ with the earlier formulas.How much did you get?
Is it something like this that you are looking for?​

 

[Alaskan Son]

How much did you get?
Is it something like this that you are looking for?

I am totally appreciative of the time you've taken. Thank you so much, but essentially I got none of it. I think I was hoping for some direction that was a little more practical and a little more physically based (for lack of better terms)--something I could do with the square, protractor, and pencil up in the right hand corner of this forum...maybe with a few minor calculations, but not so formula based. Maybe this will give you a little better idea...

I make tutorial videos for the software I use. Here are a few I've made for some geometrical challenges. I'm sure it's all pretty elementary stuff as far as you fine folks here are concerned, but this is the type of level I'm at, and the way that I think...

[YOUTUBE]IaDsqN3_VUE[/YOUTUBE]
[YOUTUBE]9hHWqtj5yBU[/YOUTUBE]
[YOUTUBE]acIaURApJzI[/YOUTUBE]...now I imagine there are some pretty complex looking formulas to describe what I've illustrated in the videos too, but what I was hoping for was something along the lines of what I've shown (draw a circle from here to here, rotate around point b, draw a line from here to here, subtract this from this, etc.). I don't know, maybe the example I've put forth is too complex for that sort of approach.

Anyway, hopefully that made sense. I apologize if my level of mathematical understanding is a bit too basic for the forum. I'd still appreciate any help I could get to simply this challenge so that I could approach it a little easier using the tools I currently have at my disposal and without going through a major re-education. If I'm being unrealistic, please let me know. Thanks again for your time.

Michael

 

[I like Serena]

I am sorry, I do not know of any way to solve your problem statement with just circles and lines.
Thank you for your videos though. They are quite instructive.
Either way, I only know how to solve your problem with equations of the appropriate unknowns and their solution.