Drawing Free-Body Diagrams: Rock Suspended by Two Strings

[fiziksfun]

My teacher asked us to draw a free body diagram for the following scenario:

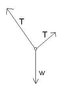
(A rock is suspended by two strings. The right string is supposed to be longer than the left one. Static)

(looks like this:)
http://i23.tinypic.com/28u7ccn.jpg

My free-body diagram looks like this:

http://i21.tinypic.com/ojmhc1.jpg

Is this right? I don't understand why the tension in the left string would be more. Help!

(P.S. how do I insert a picture?)

 

[AbedeuS]

Tension arises from the weight of the object that is being held by the string, the more vertical the string the more that downwards weight contributes to the tension, alternatively let's imagine a ball in the middle of a 2d square, attatched by 4 strings at 90 degree angles, the string at the top of the square has the highest tension, as it is holding the ball in its suspended position and its force is upwards (the force from the ball is downwards) the lowest tension string is at the bottom since the balls force is in the same direction that the string would apply its tension, unless the ball was pulling upwards due to some elastic streaching by the top string.

The side strings should potentially have no tension unless both strings were attempting the deviate the ball from a perfectly vertical position (angle them) and then the strings tension would be attributed by the strings deviating the ball from a free fall

This is just my guess on the subject though, I've never done free body diagrams.

 

[robphy]

If the object is in static equilibrium, the vector sum of all of the forces on the object will equal zero. This can be interpreted by adding those vectors tail-to-tip, and finding that the last tip meets the first tail, ... resulting in a [closed] polygon. In your case, you should find that the vectors (constrained by their directions) added tail-to-tip forms a triangle.