Alencarina
- 1
- 0
- Homework Statement
- An inclined plane shown in the figure has the acceleration intensity of a, to the right. Show that the block will slide on the plane if a > g tan ( θ - α ), where μs ( static friction) = tan θ is the static friction coefficient between the contact surfaces.
Hi, it's a simple(maybe) question.
- Relevant Equations
- F= ma
f= μN
So after trying to calculate the horizontal forces to solve it:
f + Wx(gravity force component of x) - Fy ( the Force that is supposedly giving the the acceleration) = 0
It got to me that the question said "plane has the acceleration" is that even possible? Unless the plane is another object like a ramp, but the plane itself? it's like considering the Earth's movement?!
I kept trying to prove continuing the horizontal forces. If a= g tan ( θ - α ) it means it won't move, so friction will be the μs= tan θ and the Fnet will be zero.
f + Wx - Fy =0
μN + mgcos θ - masinθ = 0
μ(mgcosθ + macosθ) - masinθ =0
And it just went on to a complex thing, I tried a couple of times, the results were close of g tan ( θ - α ), but I got to be doing something wrong.
Summarizing, could anyone tell me is the acceleration of the block or the plane? Is the block is sliding down or up (what??) and am I even close with that thought?
Figure given:
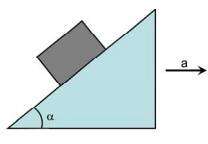
f + Wx(gravity force component of x) - Fy ( the Force that is supposedly giving the the acceleration) = 0
It got to me that the question said "plane has the acceleration" is that even possible? Unless the plane is another object like a ramp, but the plane itself? it's like considering the Earth's movement?!
I kept trying to prove continuing the horizontal forces. If a= g tan ( θ - α ) it means it won't move, so friction will be the μs= tan θ and the Fnet will be zero.
f + Wx - Fy =0
μN + mgcos θ - masinθ = 0
μ(mgcosθ + macosθ) - masinθ =0
And it just went on to a complex thing, I tried a couple of times, the results were close of g tan ( θ - α ), but I got to be doing something wrong.
Summarizing, could anyone tell me is the acceleration of the block or the plane? Is the block is sliding down or up (what??) and am I even close with that thought?
Figure given: