Eddy current damping - Analysis?

[CharleyK]

I'm trying to damp an oscillating metal plate with a neodymium magnet.

Things I know
- Remanence of the magnet
- The magnetic flux density at distance z (from the distributors site)
- Dimensions of the magnet
- Plate material (Aluminium)
- Distance to the plate.

What I'm trying to find out is the damping coefficient in the form of the Lorentz force F = -kv. I can do this with some papers I found, but I need to find the effective resistance of the plate. Now, the area below the magnet is pretty easy, but the magnetic field also passes outside of that area and I can't determine the resistance of that area (or the overall resistance on average). The two papers I found approach this with some experimental data, but it's still hazy.

Are there maybe thumb rules for this, or any got an idea how to go about this?

P.S. Here's an image to get an idea, the problem is resistance R.

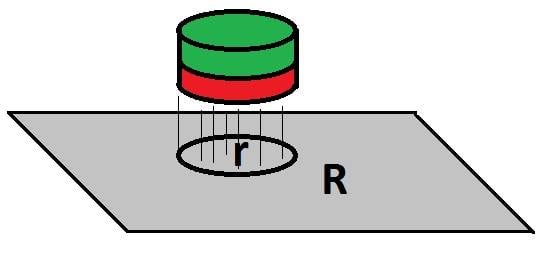
Thanks!

 

[anorlunda]

The number you are looking for is the bulk resistance of the material.

However, the effective volume of the piece is only the portion of the skin where eddy current flows. More depth --- less eddy current.

The analysis in this paper should show you how to use the data.

http://www.scielo.br/pdf/lajss/v13n11/1679-7825-lajss-13-11-01997.pdf