Discussion Overview
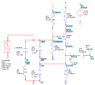
The discussion centers on the effects of coupling capacitors and inductors in an NMOS oscillator circuit, specifically a Clapp oscillator. Participants explore how the addition of a 50 Ohm load and coupling capacitors may influence the resonant frequency and overall performance of the oscillator.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions whether the coupling capacitor will affect the calculations of the resonant frequency when a 50 Ohm load is connected, suggesting that it appears in parallel with the feedback capacitor.
- Another participant suggests that traditionally, a buffer stage is used between the oscillator output and the load to avoid issues with the 50 Ohm load affecting the oscillator section.
- Some participants note that while a 50 Ohm load is generally not preferred, certain microwave oscillators are designed to work with such loads.
- Concerns are raised about the output waveform appearing as a perfect single-tone sinusoidal, with a spectrum analysis showing the second harmonic significantly lower than the fundamental, which raises questions about harmonic distortion.
- One participant proposes designing an L, Pi, or T match as a last resort for output matching to a 50 Ohm load, emphasizing the need for a buffer to mitigate load impedance effects on frequency and power output.
- Discussion includes attempts to isolate the negative resistance generator portion of the circuit and analyze its behavior, with suggestions for modeling negative resistance using an RLC circuit connected to a non-linear dependent source.
- Participants discuss the importance of verifying Barkhausen's criterion for oscillation and how load affects frequency calculations.
Areas of Agreement / Disagreement
Participants express differing views on the necessity and implications of using a 50 Ohm load with the oscillator, and there is no consensus on the best approach to coupling and buffering in this context. The discussion remains unresolved regarding the optimal configuration and its effects on performance.
Contextual Notes
Participants mention various assumptions about circuit design, including the role of buffer stages and the specific characteristics of microwave oscillators. There are unresolved mathematical steps related to the negative resistance modeling and its application in oscillator design.