rubixx14
- 1
- 0
I'm doing some modeling of a bending magnet in FEMM, to use as a magnetic spectrometer, and came across the following equation:
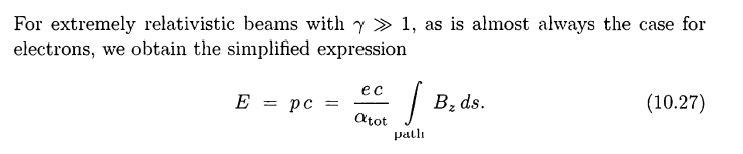
with the setup of the magnetic spectrometer similar to the following figure:
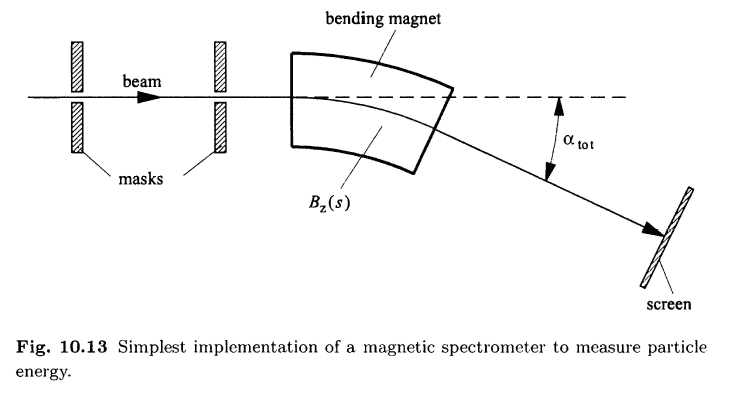
At first I modeled a hard edge scenario in a 2D cross section, where no fringe fields had been considered, and then I began to look at adding the fringe fields. My question relates to the field integral of ∫B ds and how it changes (does it increase or decrease?) when you add in the fringe fields? My initial thinking is that the integral would decrease, since the normal B field I acquired from my model decreased when I extended the path length out to include the fringe regions, but I'm not entirely confident on my conclusion.
with the setup of the magnetic spectrometer similar to the following figure:
At first I modeled a hard edge scenario in a 2D cross section, where no fringe fields had been considered, and then I began to look at adding the fringe fields. My question relates to the field integral of ∫B ds and how it changes (does it increase or decrease?) when you add in the fringe fields? My initial thinking is that the integral would decrease, since the normal B field I acquired from my model decreased when I extended the path length out to include the fringe regions, but I'm not entirely confident on my conclusion.