H Quizzagan
- 5
- 1
The set-up of the system is like the following:
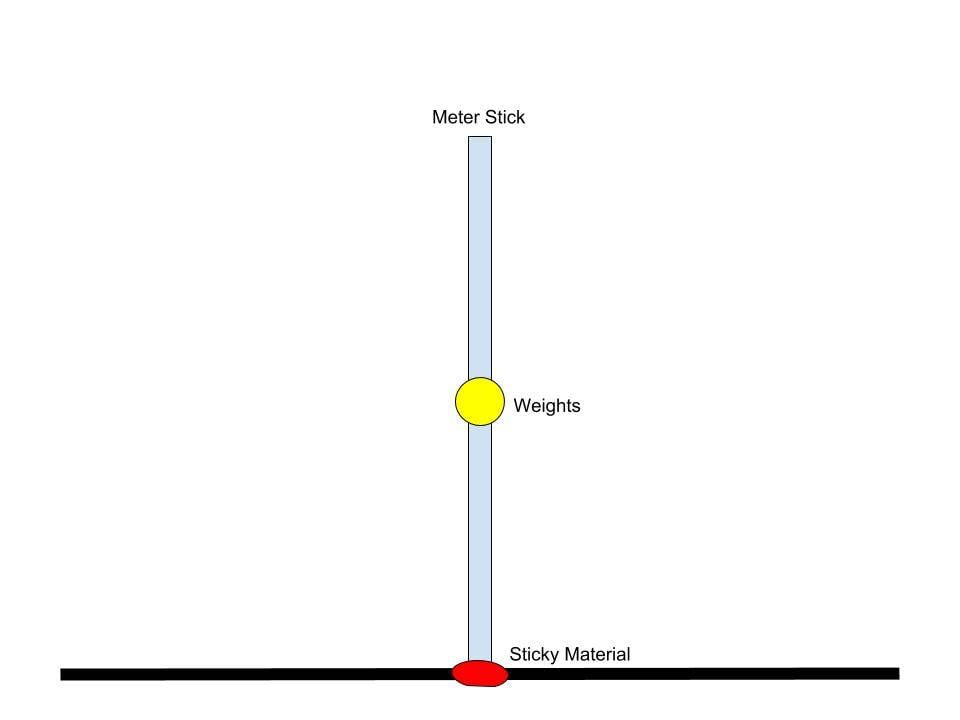
The thing is, a weight was attached to the meter stick and it was placed in different locations. Then the system composed of the meter-stick and the added weight was then released and the time it took for the meter stick to hit the floor was measured.
For the sake of simplicity, let us say it was placed in 2 different locations. This causes the Center of Gravity [CG] or Center of Mass [CM] to shift, right?
The lower the weight is, the closer to the ground the CG/CM is compared to when you place the weight higher along the meter-stick.
For each position, the amount of falling time was recorded.
QUESTION: How does the position of the CG/CM affect this quantity: falling time?
INITIAL THOUGHTS: I treated the system as a singular mass and found the CM of the entire system. Then, the motion of the CM was treated as just a free-fall so I can just use kinematics equations to calculate the total falling time.
$$ d = v_i t + \dfrac{1}{2} gt^2 = \dfrac{1}{2} gt^2 $$
So, initially, I think that as with the weights placed higher = higher location of CM = higher height to fall, means longer time to fall. Does this physics reflect anything about the reality of the system?
It is very simple I know but it got me all confused with the consideration of CM.
The thing is, a weight was attached to the meter stick and it was placed in different locations. Then the system composed of the meter-stick and the added weight was then released and the time it took for the meter stick to hit the floor was measured.
For the sake of simplicity, let us say it was placed in 2 different locations. This causes the Center of Gravity [CG] or Center of Mass [CM] to shift, right?
The lower the weight is, the closer to the ground the CG/CM is compared to when you place the weight higher along the meter-stick.
For each position, the amount of falling time was recorded.
QUESTION: How does the position of the CG/CM affect this quantity: falling time?
INITIAL THOUGHTS: I treated the system as a singular mass and found the CM of the entire system. Then, the motion of the CM was treated as just a free-fall so I can just use kinematics equations to calculate the total falling time.
$$ d = v_i t + \dfrac{1}{2} gt^2 = \dfrac{1}{2} gt^2 $$
So, initially, I think that as with the weights placed higher = higher location of CM = higher height to fall, means longer time to fall. Does this physics reflect anything about the reality of the system?
It is very simple I know but it got me all confused with the consideration of CM.
Attachments
Last edited:
