Effective masses of spring-mass systems

[ismaili]

I was asked such a question:

It is known that the effective mass of the spring in this vertical spring-mass system(figure can be viewed by the following Wiki link) is 1/3 of the mass of the spring, for example, if the mass of spring is m, and the mass of the block is M, then the period of the SHO is 2\pi\sqrt{\frac{M+m/3}{k}} where k is the spring constant.

And I found this question can be solved by the energy consideration, for example, in the Wiki demonstration:
http://en.wikipedia.org/wiki/Effective_mass_(spring-mass_system)#Vertical_spring-mass_system
Notice that there is a key step that the velocity of each position of the spring is directly proportional to its length.(which I don't know how to prove it, this is my first question.)

---

However, my second question is, Wiki said that the spring of the horizontal spring-mass system has the effective mass 0!
But I cannot understand why the above argument for solving vertical spring-mass system is not applicable here?!
This confuses me a lot.

---

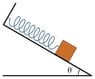
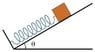
Moreover, then how about the effective masses of the such following systems? (Please see the attached plots)

 

[tiny-tim]

… there is a key step that the velocity of each position of the spring is directly proportional to its length.(which I don't know how to prove it, this is my first question.)

Hi ismaili!

This is simple geometry …
stretched length is proportional to original length, and so d/dt of stretched length is proportional to original length

my second question is, Wiki said that the spring of the horizontal spring-mass system has the effective mass 0!
But I cannot understand why the above argument for solving vertical spring-mass system is not applicable here?!

Because the weight of the spring does not affect its extension when it's horizontal

 

[ismaili]

Hi ismaili!

This is simple geometry …
stretched length is proportional to original length, and so d/dt of stretched length is proportional to original length

Hi Tim, thanks for your discussion!

"The velocity of the point of the spring is proportional to the distance of the point to the fixed end", this seems to be true only when, say, if we chop the spring into small segments, each segment stretches for the same length.
This turns out to be the case of the vertical spring-mass system, but now I guess, for other cases, this may not be true.

Because the weight of the spring does not affect its extension when it's horizontal

But the mass of the spring do play a role in the motion of the system right? My purpose is to calculate the period of such a system, from the energy consideration (in the case that the velocity of the point of the spring is proportional to the distance of that point to the fixed end):
E = \frac{1}{2}Mv^2 + \frac{1}{2}\frac{m}{3}v^2 + \frac{1}{2}kx^2
0 = Mv\frac{dv}{dt} + \frac{m}{3}v\frac{dv}{dt} + kxv=0
\left(M+\frac{m}{3}\right)\frac{d^2x}{dt^2} + kx = 0
This is basically the method to calculate the period of the system.
From this argument, even if the spring is horizontal, there exists some velocity function of the distance to the fixed end, say, v(x), then the only difference of the horizontal system to vertical one would be some change of the kinetic energy term of the spring (\frac{1}{2}\frac{m}{3}v^2 in the above case.)
If this is correct, then the effective mass of the horizontal massive spring should not be zero.

Did I mistake somewhere?
Thanks!

 

[tiny-tim]

Hi ismaili!

But the mass of the spring do play a role in the motion of the system right?
…
If this is correct, then the effective mass of the horizontal massive spring should not be zero.

sorry, I'm not understanding this at all

the weight cannot matter when the spring is horizontal;

the mass is already taken into account in the 1/2 kx² …

increase the mass (eg by adding chewing-gum) without affecting the springiness itself, and k changes proportionately

 

[ismaili]

Hi ismaili!


sorry, I'm not understanding this at all

the weight cannot matter when the spring is horizontal;

the mass is already taken into account in the 1/2 kx² …

increase the mass (eg by adding chewing-gum) without affecting the springiness itself, and k changes proportionately

If we consider the total energy of the spring-mass system, the mass of the spring would contribute a kinetic energy term.
Assume the velocity of the point x, where x is the distance of the point to the fixed end, is proportional to the x, i.e. v(x)=\frac{x}{L}v, where v is the velocity of the block, and L is the length of the spring.
Then, the kinetic energy of the spring is,
\frac{1}{2}\int_0^L\frac{dx}{L}m\left(\frac{x}{L}v\right)^2 = \frac{1}{2}\frac{m}{3}v^2.
Then differentiate the total energy equation, we get the equation of motion and we can find that the period of such a system is 2\pi\sqrt{\frac{M+m/3}{k}}.

So, as long as the spring is massive, it would contribute to the kinetic energy term, and this affects the motion.

However, in this method, we basically assumed the potential energy is still \frac{k}{2}x^2 which I kinda suspect...

 

[tiny-tim]

ismaili 1 wikipedia 0

Hi ismaili!

If we consider the total energy of the spring-mass system, the mass of the spring would contribute a kinetic energy term.
Assume the velocity of the point x, where x is the distance of the point to the fixed end, is proportional to the x, i.e. v(x)=\frac{x}{L}v, where v is the velocity of the block, and L is the length of the spring.
Then, the kinetic energy of the spring is,
\frac{1}{2}\int_0^L\frac{dx}{L}m\left(\frac{x}{L}v\right)^2 = \frac{1}{2}\frac{m}{3}v^2.
Then differentiate the total energy equation, we get the equation of motion and we can find that the period of such a system is 2\pi\sqrt{\frac{M+m/3}{k}}.

So, as long as the spring is massive, it would contribute to the kinetic energy term, and this affects the motion.

However, in this method, we basically assumed the potential energy is still \frac{k}{2}x^2 which I kinda suspect...

hmm … you seem to be right, and wikipedia is wrong!

yes, I can't see anything wrong with your reasoning …

the mass of a spring is usually ignored, because it's so small compared with the mass on the end

the main wikipedia article, at http://en.wikipedia.org/wiki/Spring_(device)#Simple_harmonic_motion, has it right …

The mass of the spring is assumed small in comparison to the mass of the attached mass and is ignored.

… but the article on effective mass, at http://en.wikipedia.org/wiki/Effective_mass_(spring-mass_system)#Horizontal_spring-mass_system, that you referred to, is wrong …

For horizontal spring-mass system, the case is simple. Since the direction of the motion of the mass and the spring is always perpendicular to the force that acting on the spring (gravity of the spring), it is no need to consider the effective mass of the spring, i.e. the effective mass of the spring is 0.

ismaili 1 wikipedia 0 ​

 

[mathrec]

The effective mass is the same in the horizontal configuration as it is in the vertical configuration. The easiest way to verify this is to examine the solution for the vertical configuration and take the limit as g -> 0. Since g is not in the formula for the effective mass...

By the way, this discussion helps address the my http://www.mathrec.org/old/2001dec/solutions.html" : Why is the effective mass for the resonance frequency M + m/3, but the static elongation of the hanging spring depends on M + m/2?