Reversible Otto Cycle Efficiency: Investigating the Difference from Carnot's

[Jacob White]

So we know that every reversible engine working between the same temperatures will have the same efficiency(the same as Carnot engine). So let's consider for example reversible Otto cycle. So as you can see on the picture it is operating between $T_1$ and $T_3$, so I was thinking that it should have efficiency $f = 1 - \frac {T_1} {T_3}$ Below there is a derivation assuming reversibility(Indeed it is reversible there is no entropy increase), however we don't get Carnot but: $f = 1 - \frac {T_1} {T_2}$ which is lower. How is it possible?

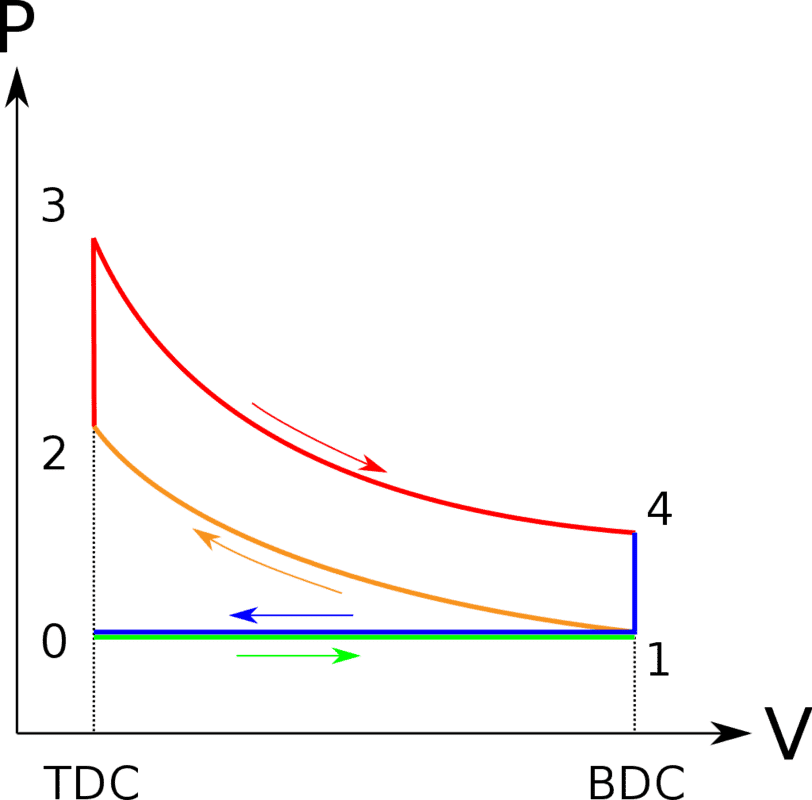https://en.wikipedia.org/wiki/Otto_cycle

 

[etotheipi]

They are different efficiencies! What you refer to is better stated that every reversible heat engine working between two heat reservoirs $T_H$ and $T_C$ have the same efficiency, the Carnot efficiency. This is what pertains to Carnot's theorem, that $\eta_{CE} \geq \eta_{X}$ with the equality only holding if the engine $X$, which also operates between two temperatures $T_H$ and $T_C$, is reversible. The Otto cycle is a different type of cycle which operates between different configuration of reservoirs.

 

[jack action]

So we know that every reversible engine working between the same temperatures will have the same efficiency(the same as Carnot engine).

That is not true. Reversible engines do not necessarily have the same efficiencies. And the Carnot cycle provides an upper limit on the efficiency that any classical thermodynamic engine can achieve during the conversion of heat into work. (Wikipedia)

 

[etotheipi]

Reversible engines do not necessarily have the same efficiencies. And the Carnot cycle provides an upper limit on the efficiency that any classical thermodynamic engine can achieve during the conversion of heat into work. (Wikipedia)

That is fine, but statement you quoted is true if we make the assertion that the heat engine necessarily operates between two heat reservoirs.

 

[Jacob White]

Ok, now I see that indeed reversible engines would have the Carnot efficiency only when working between 2 heat reservoirs at given temperatures. And with different temperatures this argument of reversing cycle and using to produce additional work just doesn't work.

 

[etotheipi]

And with different temperatures this argument of reversing cycle and using to produce additional work just doesn't work.

I don't understand this part... wouldn't reversing a cycle involve doing work on the engine to move heat from the lower temperature reservoir to the higher temperature reservoir (e.g. a refrigerator?).

 

[Jacob White]

I have said that too briefly. I have seen proof like this: If we had two heat reservoirs at T1 and T2 and two reversible engines A and B. So suppose A takes heat Q1 from T1 and doing work W1. B is also reversible so we can reverse it's cycle so it would use work W1 to transfer heat from T2 to T1. And if B would have better efficiency the same work W1 would be enough to bring back Q1 to T1 and we still have some energy to use - contradiction to second law. And then I realized that it really works only for 2 reservoirs and couldn't be generalised.

 

[etotheipi]

Cool, that makes more sense. Thanks for explaining to me!

 

[Jacob White]

Thanks for realizing me that it works only when we take heat only from 2 reservoirs!