Efficiency of Two Carnot Engines in Series

[Archduke]

Homework Statement

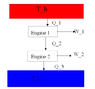
There are two Carnot engines in series, so that the heat exhaust from the first engine drives the second. Find the overall efficiency of the arrangement which contains only the efficiences of the individual engines.

Homework Equations

\epsilon = \frac{W}{Q_{input}}

The Attempt at a Solution

OK, I thought this was really easy, but it just doesn't seem right.

\epsilon = \frac{W_{1}+W_{2}}{Q_{1}} = \frac{(Q_{1} - Q_{2}) + (Q_{2} - Q_{3})}{Q_{1}} = 1 - \frac{Q_{3}}{Q_{1}}

But, surely that's saying that if you put two carnots in series that you get improved efficiency (As Q_{3} < Q_{2}), so if you put an infinite amount of carnot engines in series, you'll be able to have a 100% efficient heat engine!

So, I've either cured the world's energy problems , or I've messed up somewhere! Any hints as to where I've gone wrong? Thanks!

 

[Andrew Mason]

\epsilon = \frac{W_{1}+W_{2}}{Q_{1}} = \frac{(Q_{1} - Q_{2}) + (Q_{2} - Q_{3})}{Q_{1}} = 1 - \frac{Q_{3}}{Q_{1}}

But, surely that's saying that if you put two carnots in series that you get improved efficiency (As Q_{3} < Q_{2}), so if you put an infinite amount of carnot engines in series, you'll be able to have a 100% efficient heat engine!

You have not made any error. The efficiency of a single Carnot heat engine operating between temperatures Th and Tc is 1-Qc/Qh = 1 - Tc/Th.

You have just shown that you get the same efficiency if you put two Carnot engines in series between these two temperatures, (or any number of Carnot engines between these temperatures). The overall efficiency depends only upon these temperatures (i.e the highest and lowest temperatures involved).

The Carnot efficiency approaches 100% as Th gets arbitrarily large or Tc gets arbitrarily close to 0. But I don't see why this raises a problem. It is the same whether there are one or a zillion Carnot engines operating over that temperature range.

AM

 

[Archduke]

Oh, yes, of course! The output heat from Engine One running in series isn't the same as the output heat from the engine running alone. I see what I've done; thanks for clearing it up for me.