- #1
Master1022
- 611
- 117
- Homework Statement
- Calculate the specific net work done (work done per kg) for the cycle
- Relevant Equations
- Below
Relevant Equations:
Specific Work Done: [itex] w = \frac{p_2 v_2 - p_1 v_1}{1-\gamma} [/itex] (1)
[itex] w = \frac{R}{1-\gamma} \times (T_2 - T_1) [/itex] (2)
Thermal efficiency: [itex] \eta _{th} = 1- \frac{1}{r_p ^ {\frac{\gamma - 1}{\gamma}}} = \frac{w_{out} - w_{in}}{q_{in}} = \frac{q_{out} - q_{in}}{q_{in}} [/itex] (3)
Context & My Question:
The question was building up to us calculating the thermal efficiency of the cycle, which I can check using the above formula (equation 3).
We were given the following information about the states: (air is used so [itex] \gamma [/itex] = 1.4)
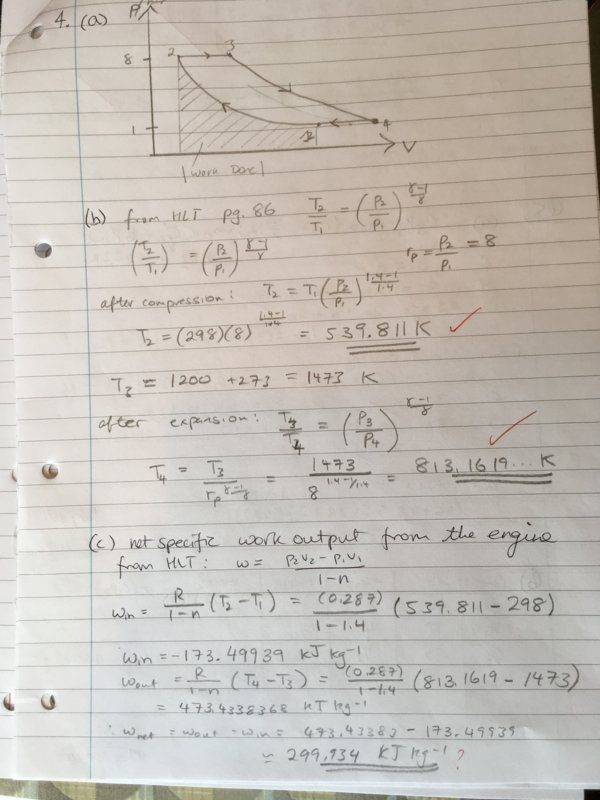
State 1 - 1 bar, 298 K
State 2 - 8 bar
State 3 - 8 bar, 1473 K
State 4 - 1 bar
Process: 1-->2: Adiabatic compression, 2-->3: Heating at constant pressure, 3-->4 Adiabatic expansion, 4--> 1 Heat rejection at constant pressure.
r_p = p2/p1 = 8
Basically, I was wondering whether anyone else could help me realize what I have done wrong when calculating the net specific work done?
I have done the previous parts of the question correctly, so I know the temperatures are correct. We don't know the specific volumes, so I opted to use the alternate form of the work done equation (equation 2). After plugging in that formula, I get the following values (kJ/kg): w_in = -173.49930 and w_out = 473.4338368, thus giving the wrong efficiency. I have found that multiplying equation (3) by [itex] \gamma [/itex] and then repeating the calculation yields the correct answer. Why is this the case? I know [itex] c_{p} = \frac{\gamma R}{1 - \gamma} [/itex], but am unable to see why we would use include that constant here.
I have used the efficiency equation with r_p the final version to calculate the efficiency correctly (should be around 0.447...)
Thanks in advance.
Pictures of my work are below:
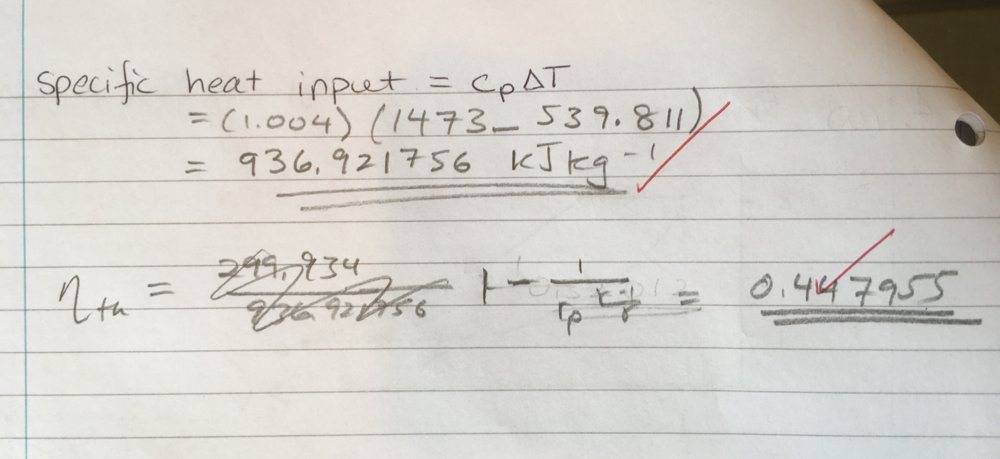
Specific Work Done: [itex] w = \frac{p_2 v_2 - p_1 v_1}{1-\gamma} [/itex] (1)
[itex] w = \frac{R}{1-\gamma} \times (T_2 - T_1) [/itex] (2)
Thermal efficiency: [itex] \eta _{th} = 1- \frac{1}{r_p ^ {\frac{\gamma - 1}{\gamma}}} = \frac{w_{out} - w_{in}}{q_{in}} = \frac{q_{out} - q_{in}}{q_{in}} [/itex] (3)
Context & My Question:
The question was building up to us calculating the thermal efficiency of the cycle, which I can check using the above formula (equation 3).
We were given the following information about the states: (air is used so [itex] \gamma [/itex] = 1.4)
State 1 - 1 bar, 298 K
State 2 - 8 bar
State 3 - 8 bar, 1473 K
State 4 - 1 bar
Process: 1-->2: Adiabatic compression, 2-->3: Heating at constant pressure, 3-->4 Adiabatic expansion, 4--> 1 Heat rejection at constant pressure.
r_p = p2/p1 = 8
Basically, I was wondering whether anyone else could help me realize what I have done wrong when calculating the net specific work done?
I have done the previous parts of the question correctly, so I know the temperatures are correct. We don't know the specific volumes, so I opted to use the alternate form of the work done equation (equation 2). After plugging in that formula, I get the following values (kJ/kg): w_in = -173.49930 and w_out = 473.4338368, thus giving the wrong efficiency. I have found that multiplying equation (3) by [itex] \gamma [/itex] and then repeating the calculation yields the correct answer. Why is this the case? I know [itex] c_{p} = \frac{\gamma R}{1 - \gamma} [/itex], but am unable to see why we would use include that constant here.
I have used the efficiency equation with r_p the final version to calculate the efficiency correctly (should be around 0.447...)
Thanks in advance.
Pictures of my work are below:
Last edited: