Effort Required to Overcome Inertia

[sriram123]

hi all,
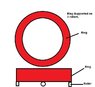
This is a question regarding calculation of effort required to over come the inertia of a body.Let us have a ring(Some random example) which is supported by three rollers(Ring is sitting on the rollers).To rotate the ring,the applied effort has to overcome the friction and inertia of the body.The frictional force can be calculated using the coefficient of friction for line contact and the normal reaction (Weight of the body).But to calculate the force to overcome inertia mass of the body and the acceleration of the body has to be considered.This "acceleration " part that is quiet confusing to me.
How can I calculate the acceleration if I Manually push the ring.For example,I know how much distance I have to push(The circumference if I make one complete rotation),The time for rotation and that the initial velocity is zero(For first rotation).Can I use Equations of motion ( s=ut+0.5at^2) to find the acceleration which I can use in the Calculation of Inertial force?.

If I am too confusing,Simply put I want to know how to calculate the force required to overcome the inertia of a body If i know mass,distance to travel,time and initial velocity.

I am just trying to understand the concept so don't mistake me if i have misstated something.

Sorry for attaching a crappy image.I am on summer vacation and I only have paint installed in this computer(Even with paint many can do better but I can't)
Thanks in advance.

 

[tiny-tim]

hi sriram123!

(btw, the image looks fine to me!)

… .But to calculate the force to overcome inertia mass of the body and the acceleration of the body has to be considered.This "acceleration " part that is quiet confusing to me.
How can I calculate the acceleration if I Manually push the ring.For example,I know how much distance I have to push(The circumference if I make one complete rotation),The time for rotation and that the initial velocity is zero(For first rotation).Can I use Equations of motion ( s=ut+0.5at^2) to find the acceleration which I can use in the Calculation of Inertial force?.

If I am too confusing,Simply put I want to know how to calculate the force required to overcome the inertia of a body If i know mass,distance to travel,time and initial velocity.

(i assume you're only interested in rotating the ring, "on-the-spot"?)

please stop thinking about "overcoming the inertia"

there's no such thing as inertia … there's moment of inertia, and a couple of other phrases, but inertia on its own doesn't mean anything (or it just means "mass")

the mass isn't something that has to be "overcome" like a friction force or an energy threshold

a mass starts moving as soon as you push it (subject to friction etc)

the only equations you need are F = ma and τ = Iα

(and the standard constant acceleration equations, with θ ω and α instead of s v and a)​

 

[Nugatory]

The only equation you need to understand how force overcomes inertia is F=ma; and note that a is acceleration, which is the change in speed.

So no matter how large the mass or small the force, any net force will produce some acceleration. If the mass is moving at a constant speed the acceleration is zero so the net force is zero; if you're still pushing it to keep it moving then all of the force you're applying is exactly balancing the force of friction to end up with zero net force.

Your ring problem is a bit harder because it involves rotation so requires that you work with torque and the moment of inertia. Thus you might want to be sure that you understand the "effort required to overcome inertia" problem in the simpler case of a block sliding at a constant velocity on a flat surface with friction, before you take on the rotating ring.