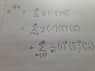Eigenvectors of exponential matrix (pauli matrix)

[Punctualchappo]

Homework Statement

Find the eigenvectors and eigenvalues of exp(iπσ_x/2) where σ_x is the x pauli matrix:
10
01

Homework Equations

I know that σ_xⁿ = σ_x for odd n
I also know that σ_xⁿ is for even n:
01
10

I also know that the exponential of a matrix is defined as Σ(1/n!)xⁿ where the sum runs from n=0 to infinity

The Attempt at a Solution

Using knowledge of the matrix exponential, I can say that exp(iπσ_x/2) = Σ(1/n!)(iπσ_x/2)ⁿ. I can then split this into two sums, one for even n and one for odd n. This allows me to take the power off the matrices for easier summing. It's then that I get stuck. I've attached a file showing the two sums because it's easier and clearer to show you this way.[/B]

I'd really appreciate any help that can be given.

 

[Punctualchappo]

I've realized that when written as the two sums, it's clear that there are only two linearly independent eigenvectors for each sum. I'm not sure how it works when the i's get multiplied in though. Aren't there infinite eigenvalues to reflect the infinite nature of the sums?

 

[BvU]

Hi chap, welcome to PF :),

What would an eigenvector of exp(iπσ_x/2) look like ? What conditions would it have to satisfy ?

And what about eigenvectors of σ_x itself ?

 

[Punctualchappo]

So the eigenvectors would have to satisfy exp(iπσ_x/2)v = Av where A is the eigenvalue. I know that eigenvectors of σ_x are (1,1) and (1,-1)
Thanks for your help.

 

[HalfLostAndSearching]

Hello, thank you for your question. I would approach this problem by first understanding the properties of eigenvalues and eigenvectors of a matrix. The eigenvalues of a matrix are the values that, when multiplied by the identity matrix, give back the original matrix. Eigenvectors are the vectors that, when multiplied by the matrix, give back the original vector multiplied by the eigenvalue.

In this case, we are dealing with the exponential matrix of the Pauli matrix σx. The first step would be to find the eigenvalues of σx, which are ±1. This means that when we multiply σx by ±1, we get back the original matrix.

Next, we can use the properties of the exponential matrix to simplify the problem. The exponential of a matrix is defined as the sum of the matrix raised to different powers. In this case, we can use the property that σxn = σx for odd n. This means that all odd powers of σx will give back the original matrix.

Using this knowledge, we can rewrite the exponential matrix as exp(iπσx/2) = Σ(1/n!)(iπσx/2)n. We can then split this into two sums, one for even n and one for odd n. For the even powers, we can use the property that σxn is equal to the identity matrix. This means that all even powers of σx will give back the identity matrix.

For the odd powers, we can use the property that σxn = σx. This means that all odd powers of σx will give back the original matrix. In this case, we can rewrite the odd powers as σx = σx.

Now, we can simplify the sums and solve for the eigenvalues and eigenvectors. We know that the eigenvalues are ±1, so we can substitute these values into the sums and solve for the eigenvectors. The eigenvectors for the eigenvalue 1 are [1 0]T and the eigenvectors for the eigenvalue -1 are [0 1]T.

In conclusion, the eigenvectors of the exponential matrix exp(iπσx/2) are [1 0]T and [0 1]T, with corresponding eigenvalues of 1 and -1, respectively. These eigenvectors and eigenvalues satisfy the properties of eigenvalues and eigenvectors