Phinrich
- 82
- 14
- TL;DR
- What is the connection, if any, between the Einstein Tensor and the Stress-Energy Tensor of a Scalar Field ?
Hi All.
Given that we may write
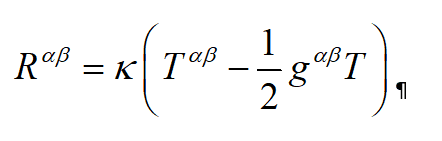
And that the Stress-Energy Tensor of a Scalar Field may be written as;
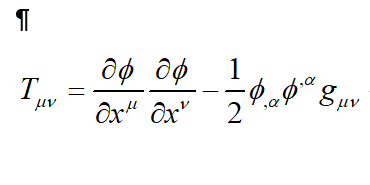
These two Equations seem to have a similar form.
Is this what would be expected or is it just coincidence?
Thanks in advance
Given that we may write
And that the Stress-Energy Tensor of a Scalar Field may be written as;
These two Equations seem to have a similar form.
Is this what would be expected or is it just coincidence?
Thanks in advance