Electric Field and Voltage Equation Applications

[freddy13]

I have two questions!

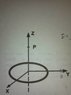
General: A uniform circular ring of charge Q and radius R is located in the x-y plane, centered on the origin as shown in the figure.

#1 What is the magnitude of the electric field, E, at point P located a distance z above the center ring?

I came up with kQ/(R^2 + z^2). I would like to know if this is correct or where I went wrong, and how to disprove other answers!

#2 What is the voltage at location P, assuming the voltage at infinity is zero?

Any help is appreciated! Thanks in advanced!

 

[mfb]

I came up with kQ/(R^2 + z^2). I would like to know if this is correct or where I went wrong, and how to disprove other answers!

Which electric field do you expect in the center of the ring? Does your equation give the same result?

#2 What is the voltage at location P, assuming the voltage at infinity is zero?

And your attempt to solve the problem?