guyvsdcsniper
- 264
- 37
- Homework Statement
- A sphere with radius R has a volume charge density
ρ = ρ0 𝑟⁄𝑅, where ρ0 is constant.
Find the electric field as a function of r, from r=0 to infinity.
- Relevant Equations
- Eda=qenc/epsilon
Im having trouble understanding the wording to this problem. When it says "from r=0 to r=infinity". My Qenc would zero out. I guess it makes sense that from infinitely far away you wouldn't "feel' the electric field but considering this question leads to 4 other questions I don't think I am approaching this right.
Can anyone help me understand this a little better?
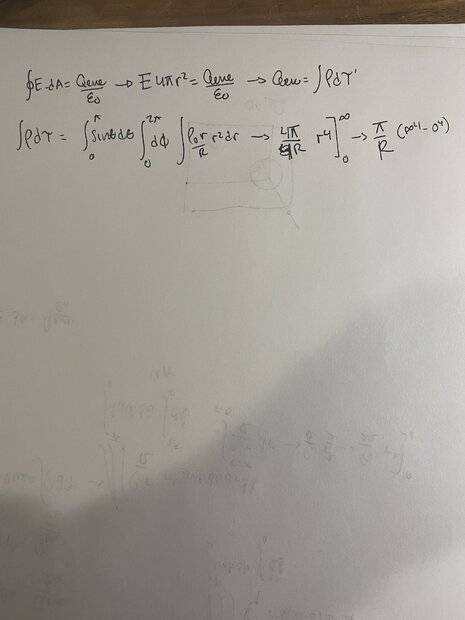
Can anyone help me understand this a little better?