Electric field due to a line of charge

[Gee Wiz]

Homework Statement

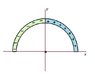
The charge configuration at the right consists of an insulating rod that is bent into the shape of a quarter-circle having total positive charge Q distributed uniformly over its length. Suppose that the magnitude of the total electric field at the origin due this charge configuration is E0.
In terms of E0, what would be the total electric field vector at the origin due to the semi-circle of charge shown below? The left quarter-circle has negative charge, -Q, distributed uniformly and the right quarter-circle has positive charge, Q, distributed uniformly.

Homework Equations

The Attempt at a Solution

Well for this one since the charges on the two halves of the semi circle are opposite I know that the object doesn't move in the vertical (y) direction. I also know from the charges that it moves to the left or negative x direction. But i do not know how to get the value for this problem. The answer is -√2*Eo

 

[TSny]

Well for this one since the charges on the two halves of the semi circle are opposite I know that the object doesn't move in the vertical (y) direction. I also know from the charges that it moves to the left or negative x direction. But i do not know how to get the value for this problem. The answer is -√2*Eo

Hello Gee Wiz.

Can you clarify what "object" you are referring to here? Note that there is nothing at the origin except electric field. Can you see what the direction of E would be from each quarter-circle of the semi-circle?

 

[Gee Wiz]

by object i mean like a point charge. (yes i know there isn't one there, its just how i visualize things)

 

[Gee Wiz]

Well from the E field on the right with the positive Q would point away from the line, and the E field on the left with the negative Q would point towards the line. By line i mean the part of the semi circle

 

[TSny]

What is the angle between the net electric field due to the left quarter-circle and the net electric field due to the right quarter-circle?

 

[Gee Wiz]

I'm don't fully understand your question. My gut tells me that the angle is always changing depending where on the semi-circle you pick...but that doesn't seem right to me.

 

[TSny]

Right, each little bit of charge on the semi-circle would produce an electric field at the origin that would have a direction that would vary as you pick different bits of charge. But, suppose you consider the entire quarter-circle of negative charge. Just using "symmetry arguments" can you deduce the direction of the total electric field due to all the bits of charge in that quarter-cricle?

 

[Gee Wiz]

It would just be in the negative x-direction (along the x-axis)

 

[TSny]

It would just be in the negative x-direction (along the x-axis)

I'm assuming the setup is as shown in the attachment. Hope I got it right.

The negatively charged part of the ring will produce a total electric field in what direction at the origin?

 

[Gee Wiz]

Well the negatively charged part would produce an electric field going along the line y=-x?

 

[Gee Wiz]

or well in the negative x direction, positive y direction. Field lines point toward the negative charges.

 

[TSny]

or well in the negative x direction, positive y direction. Field lines point toward the negative charges.

Yes. Good. And you know what the magnitude of that field is, right?

Now do the same reasoning for the positively charged part of the semicircle?

You'll then need to add the field of the negative part to the field of the positive part (vector addition).

 

[Gee Wiz]

The Field from the positive charge points in the negative x direction and negative y direction. Field lines away from the positive charge. I believe the magnitude of each one would just be Q? If i add the negative part of the field to the positive part I find that the y-direction cancels out, but I'm not sure how to get the x direction. What vectors would i be adding, i don't think i am visualizing those correctly

 

[TSny]

The problem states that the magnitude of a quarter-circle is Eo. So you have two vectors, each of magnitude Eo. You know that the vector representing the field from the negative part points to the left and up. Can you specify the angle it makes to the x-axis? Can you use that angle to find the x-component of the the field from the negative charge (expressed in terms of Eo)?

You are correct that the total y-component of field from the entire semicircle will be zero.

 

[Gee Wiz]

Oh, okay so i can almost just picture two vectors of length Eo going/coming from (depending on which charge) the origin. With an angle of 45 degrees. Then with trig if i take the cosine of that i get Eo*(root2)/2 for one of them. I then double this (because of the two vectors, or well i guess add) to get my final answer of (root2)Eo

 

[TSny]

That sounds right. Good work.

 

[Gee Wiz]

Awesome, thank you so much for your time and explanation. It was very helpful