utkarshakash
Gold Member
- 852
- 13
Homework Statement
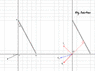
A non-conducting rod AB, having uniformly distributed positive charge of linear charge density λ is kept in x-y plane. The rod AB is inclined at an angle 30° with +ve Y-axis. The magnitude of electrostatic field at origin due to rod AB is E_0 N/C and its direction is along line OC. If line OC makes an angle θ=10a+b degree with negative x-axis as shown in the figure, calculate the value of (a+b) [OA=2m and λ=10^3 C/m]
Homework Equations
Please see the attached diagram
The Attempt at a Solution
E_x = \dfrac{\lambda}{4 \pi \epsilon _0 d} (\sin 60 + \sin 30) \\<br /> E_y = \dfrac{\lambda}{4 \pi \epsilon _0 d} |\cos 30 - \cos 60| \\<br /> <br /> \tan \alpha = \dfrac{E_y}{E_x} \\<br /> =\dfrac{ |\cos 30 - \cos 60| }{(\sin 60 + \sin 30)}
which comes out to be 15°.
Thus, θ = 30° - 15° = 15°. So, a+b = 6. But it's not the correct answer :(